内容に関するQ
|
A
|
【クレローの定理】
・ どの星でも成立するのでしょうか?また成立とするとして、どの星でも引力と遠心力の比は同じオーダーなのでしょうか(水越) |
成り立たない星があるとすれば、高速回転する中性子星などでしょうか?比については、月、金星、水星の自転速度を考えれば分かるように、地球と同じオーダーでないでしょう。 |
【基本定数-1】
・基本定数を定めるときには、様々な人が様々なことをいうと思いますが、最終的にはどのようにきめるのですか?(中山)
・基本定数に端数がないのはなぜか?また、更新されることはないのか(楠) |
・国際測地学協会(International Association of Geodesy)が、専門委員会を作り、そこで案を作成し、総会で決議します。
・端数があるということは、無限に小数が続くということですから、「決議」に困るわけ。
・更新されることはあります。GRS80の前は、GRS67というのがあったと記憶。 |
【基本定数-2】
J2は無次元量ではないと思うのだが、なぜGRS80では無次元なのか?(芋生) |
J2は無次元量です。引力ポテンシャルを球面調和関数展開したときの2次の係数ですが、(GM/r)で規格化されています。 |
【擾乱ポテンシャル-1】
・どのような実用上のメリットがあるのか?(彦坂)
・物理的な意味が分からなかった(左高)
・代表的なソースを知りたい(山浦) |
擾乱ポテンシャルがあれば、現実の重力ポテンシャルが表現できるということです。現実の重力ポテンシャルが精密に分からなければ、GPS衛星の軌道計算も出来ないので、スマホで自分の位置を高い精度で知ることも出来ないし、飛行機のオートパイロットも困難になります。 |
∇2W - ∇2U = 2ω2-2ω2=0
となる理由がわからなかった。(赤玉) |
(2.1.4)式から ∇2W =2ω2 (外部ではρ=0)。いいかえれば、2ω2は、遠心力ポテンシャルのラプラシアン。正規重力ポテンシャルUも引力ポテンシャルVと遠心力ポテンシャルの和だから、∇2U =∇2V + 2ω2=0+2ω2 |
【Brunsの式】
・ 2階微分の項は無視できるのか?(西山)
・(∂U/∂h)の"h"の定義は?(横谷) |
・ γ=980 [gal]=9.8 [m/sec2 ], |N| 〜数十 [m]を考えると
展開の1次項(つまりBruns)の大きさは数百[m2/sec2 ]。
一方、Taylor 展開2次項は
(∂2U/∂h2)N2/2=(∂γ/∂h)N2/2 、
(∂γ/∂h)=0.3086 [mgal/m]=3.09E-5[/sec2] から、
展開2次項の大きさは最大でも0.015 [m2/sec2 ]。すなわち
Bruns式の10万分の1程度で、無視できます。
・ hは、楕円体面に立てた垂線方向の距離(楕円体高)です。 |
【スカラー重力異常】
なぜ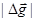 ではなくて、gP-γQなのですか?(増田) ではなくて、gP-γQなのですか?(増田) |
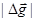 を知るには、当然、垂直線偏差(重力ベクトルを基準にしたときの、楕円体法線ベクトルのズレの角度)が必要となりますが、10〜20"角程度の量の天文観測を多数の点で行うことが困難だったからでしょう。それに比べると重力の大きさだけを測るほうは比較的容易。 を知るには、当然、垂直線偏差(重力ベクトルを基準にしたときの、楕円体法線ベクトルのズレの角度)が必要となりますが、10〜20"角程度の量の天文観測を多数の点で行うことが困難だったからでしょう。それに比べると重力の大きさだけを測るほうは比較的容易。 |
【ジオイド高-1】
・エリプソイドからジオイドまでの距離を用いて、地球の内部密度を求めるという試みはなされているでしょうか?(湯本)
・世界的なジオイド高の分布を決める要因には、何が最も影響をあたえているのですか?(冨田) |
良い視点です。
たとえば海溝沿いにジオイドが凹んでいるということは、そこではアイソスタシーが成り立たず、プレートの沈み込み(重いスラブの沈み込み)が続いていることをしめすのでしょう。また、マントル対流による密度場のモデル計算をジオイドと比較する試みなどがあります。 |
【ジオイド高-2】
ジオイド高は季節によっても変化するか?(石塚) |
季節変動は検出されていません。東北地震による地球内部変動で東北沿岸で最大2cm程度のジオイド高変化は計算により予測されています。 |
【ジオイド高-3】
日本海側でジオイド高の勾配が急になっているが、海面はどの程度これにそっているのか?(岡) |
平均海面とジオイドとのズレの程度は、20cmぐらいだと思います。 |
【球近似】
擾乱ポテンシャルを付加して、現実のポテンシャルを再現しようとする中で、球近似により
どのぐらい現実と乖離しているかが気になりました(湯本)
球近似の解と真の解との誤差が1/300というのは数学的に示してもそうなるでしょうか?(横田) |
原理的には、摂動法と同じ考えです。境界条件に少し擾乱を与えたら、解がどれだけ動くかという問題です。 |
【Stokes積分】
エリプソイド座標では解くことができないのでしょうか?(横尾) |
・う〜ん。面白い考えです。擾乱ポテンシャルTの展開係数のところまでは出来るかもしれない。しかし、積分表現にして積分核を求めるのは無理そう。 |
【Stokes積分】
現代において、球近似をせずに数値計算した例はあるのでしょうか。またそれは役に立つのでしょうか?(池端) |
Molodennskyのテルロイド理論というのがあります。 |
【重力擾乱ベクトル】
どういった場合につかいますか?(久住、加藤、楠) |
GPS等の進化により、地上の観測点の(x、y、z)座標や、楕円体に対する緯度、経度、高さ(楕円体高)が簡便に得られるようになってきました。ですから、重力異常に代わって重力擾乱に基づくStokes積分もどきも可能となってきました。 |