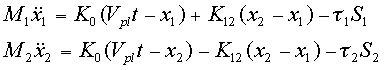
[1] 次期建議では,「1. 地震発生に至る地殻活動解明のための観測研究の推進」の4つの柱のひとつとして「(4)地震発生の素過程」に関する理論的・実験的研究を推進することになった.本稿では,最近の成果であるプレート境界での様々なすべりモードの発見,およびその多様性に関する摩擦構成則に基づく解釈を踏まえ,次期計画で「地震発生の素過程」の研究をどのように推進しようとしているかについて述べる.
[2] 現予知研究計画の大きな成果のひとつは,大地震を起こすアスペリティ,余効すべり,間欠的な非地震性すべりなど,プレート境界におけるすべりモードの多様性を明らかにしたことである.また,それらの異なるすべりモードを起こす領域が棲み分けているらしいこともわかってきた.
1) アスペリティモデル
[3] 断層面上で,地震時以外は固着しており準静的すべりが起こらず,地震時に大きく高速にすべる領域をアスペリティと呼んでいる.最近の研究により,アスペリティは領域固有の性質であることがわかってきた.プレート境界には地震の数サイクルにわたって位置やサイズを変えずにアスペリティが分布しており,そのようなアスペリティで高速すべりが起こって地震が発生する.三陸沖のプレート境界においては,ひとつだけ破壊した場合M7クラスの地震になるアスペリティがいくつか分布しており,地震の大きさ(破壊の最終サイズ)はいくつのアスペリティが連動して破壊するかで第1次近似的には決まっているらしい.
[4] この捉え方が正しければ,大地震の発生予測に希望をもたらす.地震予知の3要素,地震が「いつ」「どこで」「どのくらいの規模」で起こるのか,のうち「どこで」はあらかじめ決まっていることになるからである.「どのくらいの規模」かについても,連動して破壊するアスペリティが1個なのか,2個なのか,というようにかなり絞れる.残りの要素である「いつ」については,ターゲットとするアスペリティを見張っていれば,応力の蓄積,プレスリップなどから長期・中期的予測の精度をあげていくことができるかもしれない.もちろん「どこで」次の地震が起こるか予測することは,全てのアスペリティについて「いつ」破壊するかを予測して初めてできることであり,そのようなことは不可能であろう.
[5] そのようなアスペリティモデルの対極として,毎日あちこちで起こっている微小地震がたまたま大地震に発展する,という捉え方がある.その場合,最終破壊サイズは数百mなのか数十kmなのか,オーダーの予測も困難である.それに対し,アスペリティモデルにおいては,アスペリティの連動性は複雑であることがわかってはいるものの,アスペリティが1個破壊するのか,2個なのか,ファクターの予測を目指していけばよい.ただし,アスペリティが領域固有の性質で保存されていることを示唆するデータはまだ僅かしか得られていないので,現段階で一般化するのは危険である.アスペリティの実体を明らかにすることが次期計画でやるべき重要な課題である.
2) 様々な準静的すべり
[6] 東海地域のプレート境界で2001年から非地震性すべりが続いていることが国土地理院GPSにより検出された(1).また,過去にもそのような非地震性すべりが起こっていたことを示す地殻活動データに基づき,東海地域における非地震性すべりは間欠的に繰り返し発生していた可能性が示された(2).この間欠的非地震性すべりは他のイベントにトリガーされて起こるような現象ではないが,大地震が起こったあと,地震を起こしたアスペリティに隣接する領域で余効すべり(非地震性のゆっくりしたすべり)が数ヶ月から数年続く現象も数箇所で見出された.
[7] プレート境界で発見された,このような様々なすべりモードは,異なる摩擦パラメータをもつ領域間の相互作用の結果として説明できることが,室内実験や数値シミュレーションによって示されてきている.相互作用を直接扱える最小のシステムはふたつの要素からなるシステムである.次節で,ふたつのブロックからなるモデルを用いた数値シミュレーションについて紹介する.
[8] 図1(a)で示したように,ふたつのブロックとバネ定数K0のバネでつながれているドライバーを一定のゆっくりしたスピードVplで引っ張るモデルを考える.ふたつのブロック(ブロック1とブロック2)はK12のバネでつながられているとする.運動方程式は次のように書ける.
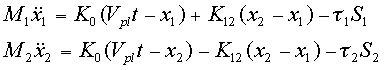
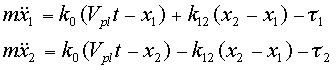
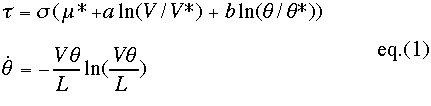
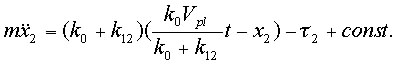
kc=(B-A)/L>k0+k12 eq.(2)
のときは不安定であり動的すべりが生ずる.一方a-b<0でかつ
kc=(B-A)/L<k0+k12 eq.(3)
のときは条件つき安定,すなわち,大きな擾乱を受けたときには不安定破壊(動的すべり)が生じるが,そうでないときは安定すべりを続ける(4).
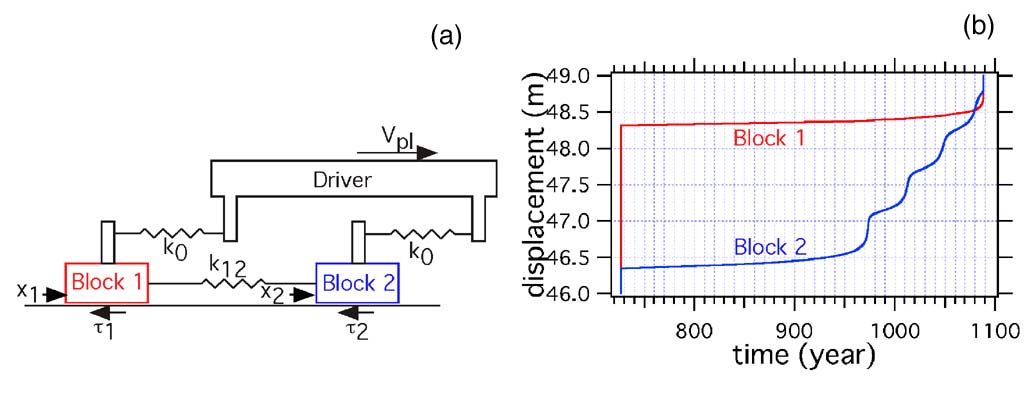 図1.
(a) ふたつのブロックモデル.(b) ブロック2が安定ー不安定遷移領域にあるとき,間欠的な非地震性すべりが起こる.
図1.
(a) ふたつのブロックモデル.(b) ブロック2が安定ー不安定遷移領域にあるとき,間欠的な非地震性すべりが起こる.
[9] 図2では,横軸に(b-a) σ, 縦軸に臨界すべり変位Lをとり,安定・不安定境界を表わすk= k0+k12= (b-a)σ/Lの直線が太線で示されている. a-b<0のときは,同じLの場合,(b-a)σが大きいほど(応力降下量が大きくなり)不安定性が強くなる.ここでσは法線応力ー間隙水圧なので,間隙水圧が高い方が安定になる.同じ(b-a)σのときは,Lが小さいほど,僅かにすべっただけで摩擦が大きく減少するのでより不安定になりやすい.Yoshida and Kato (2003)(5)は,ブロック1の摩擦パラメータはeq.(2)を満たすように設定し,ブロック2のパラメータを様々に変えて数値シミュレーションを行った結果,多様なすべりモードの棲み分けが摩擦パラメータによって規定されており,パラメータ空間上で図2のように4つのregimeに分類できることを示した.
regime1:k>kcでありアスペリティとして振る舞う.自ら動的破壊に移行するポテンシャルを有しており,動的破壊の前にプレスリップが生ずる.
regime 2:k< kcであるが,安定・不安定境界に近い.隣りのブロックが動的破壊を起こすとトリガーされて応力降下を伴う動的すべりを起こす(図1(b)).その後固着しているが,応力があるレベルまで蓄積すると,定常値の周りですべり速度や応力が振動を始め,やがて定常状態へ収束していく.図では,定常状態に収束する前に次の動的すべりがトリガーされている.このような間欠的な非地震性すべりが,東海地域で検出されている準静的すべりに対応しているかもしれない.
regime 3:regime 2と本質的には同様の振舞いをするが,振動することなく定常状態にスムーズに収束する.
regime 4:a-b>0であり,固着ステージがない.隣りのブロックの動的すべりにより急激に応力荷重がなされ,その応力を緩和しながら余効すべりを起こす.相互作用が強い場合,隣りのブロックがすべるとつられて動的すべりを起こすこともある.
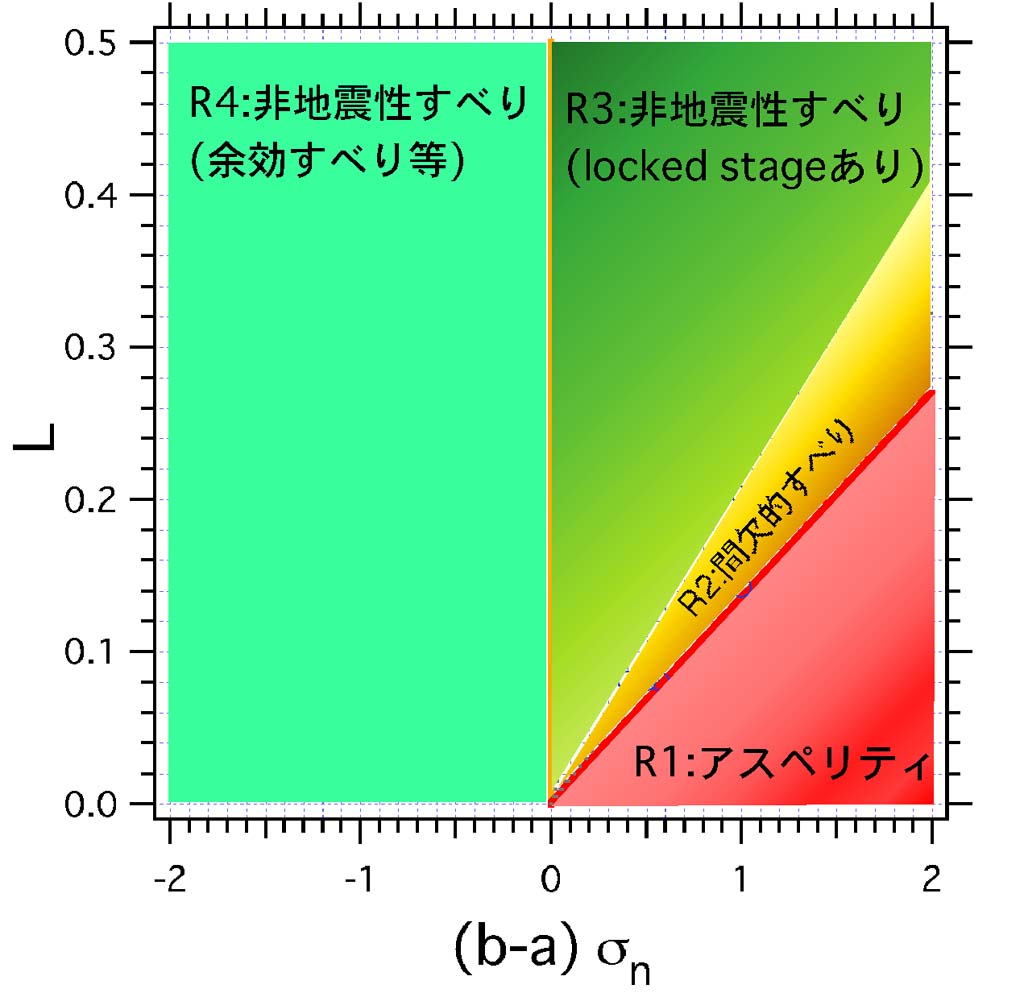 図2.
摩擦パラメータによって決まる多様なすべりモード.
図2.
摩擦パラメータによって決まる多様なすべりモード.
[10] なおここでは,少なくともひとつのブロックがアスペリティであることを前提にしており,アスペリティの動的すべりがシステムを周期的に不安定にしている.システムがアスペリティを含まない場合は,ふたつのブロックが単に安定すべりを続けるだけになり,多様なすべりモードは現れない.また,ふたつのブロックの底面積が等しい(S1=S2)と仮定したが,仮にS1<S2である場合を考えてみると,ブロック1への相互作用はK12/S1,ブロック2へはK12/S2のバネでもたらされるので,大きなブロックから小さなブロックへの影響が強く,逆に小さなブロックから大きなブロックへはあまり影響を与えないことわかる.
[11] 上記の分類の一部は室内実験でも確かめらている.大型剪断試験機を用い,長さ1mの花崗岩の模擬断層面に摩擦特性の異なる領域を分布させ,すべり実験を行った結果を記す(6).模擬断層面のうち,半分の50cmの領域に薄いテフロンシートを挟み速度・状態依存摩擦構成則パラメータのa-bが正となるようにし,残り半分の領域は花崗岩どうしを直接接触させa-bが負となるようにした(図3).断層に沿って多数の変位計と歪ゲージをセットし局所的なすべり変位と剪断応力を測定した. a-b<0の領域はアスペリティ的に振舞い,固着すべりを起こし,a-b>0の領域では,アスペリティでの動的すべりにより応力が急激に上がり,それを緩和しながら顕著な余効すべりが起こった(図4).この非地震性すべり領域でも,アスペリティでの動的すべりに連動し地震時すべりを起こすが,地震時すべり量はアスペリティから離れるほど小さくなっている.
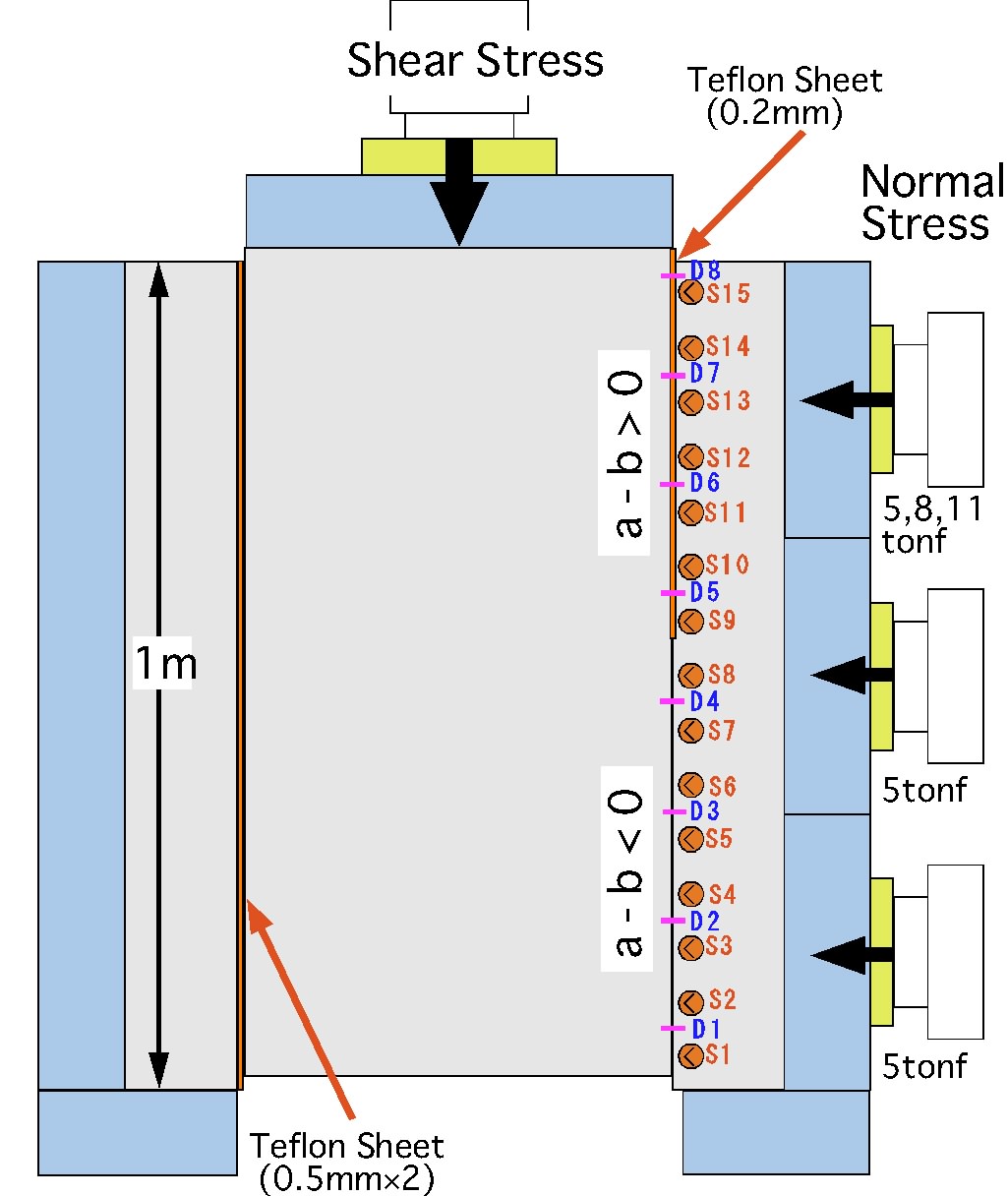 図3.
大型剪断試験機.
図3.
大型剪断試験機.
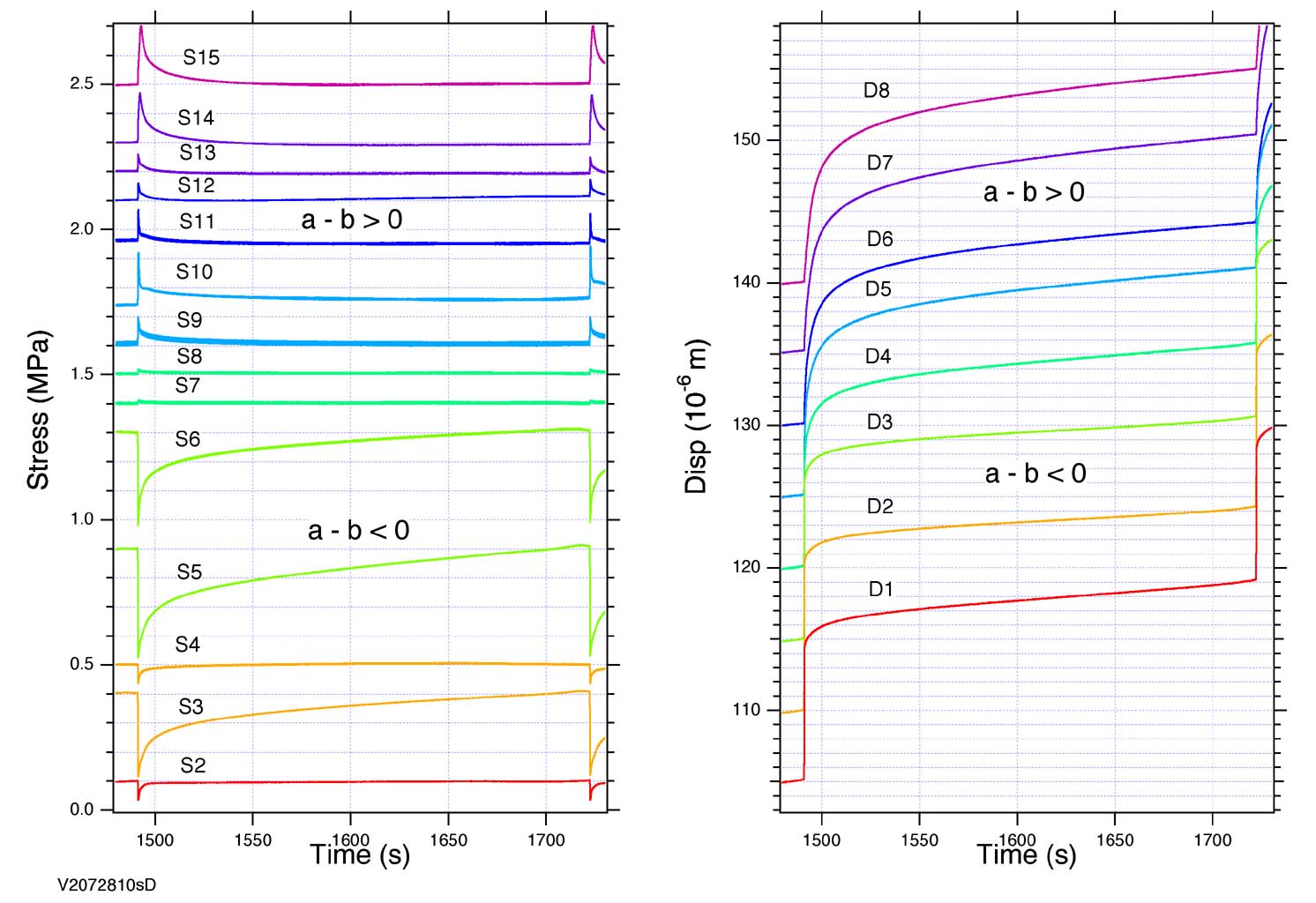 図4.
大型剪断試験機によるすべり実験で得られた,局所的なすべり変位(右図)と剪断応力(左図).a-b<0の領域(D1-4, S2-6)はアスペリティ的に振る舞う.a-b>0の領域(D5-8, S9-15)では,アスペリティでの動的すべりにより応力が急激に上がり,それを緩和しながら余効すべりが起こっている.
図4.
大型剪断試験機によるすべり実験で得られた,局所的なすべり変位(右図)と剪断応力(左図).a-b<0の領域(D1-4, S2-6)はアスペリティ的に振る舞う.a-b>0の領域(D5-8, S9-15)では,アスペリティでの動的すべりにより応力が急激に上がり,それを緩和しながら余効すべりが起こっている.
(略)
(略)
| 1. | Ozawa, S., M. Murakami, M. Kaidzu, T. Tada, T. Sagiya, Y. Hatanaka, H. Yarai, and T. Nishimura, Detection and monitoring of ongoing aseismic slip in the Tokai region, central Japan, Science, 298, 1009-1012, 2002. |
| 2. | 木俣文昭・藤井直之・平原和朗,上下変動と辺長変化から推定する1987年東海スロースリップ,地震学会予稿集秋季大会, A41, 2001. |
| 3. | 吉田真吾,実験室で地震を探る,菊地正幸編「地殻ダイナミクスと地震発生」,140-162, 朝倉書店,2002. |
| 4. | Scholz, C. H., The mechanics of earthquake and faulting, 433 pp., Cambridge Univ. Press, New York, 1990. |
| 5. | Yoshida, S., and N. Kato, Episodic aseismic slip in two degree-of-freedom block-spring model, Geophys. Res. Lett., 30, doi:10.1029/2003GL017439, 2003. |
| 6. | 吉田真吾・中谷正生・加藤尚之・加藤愛太郎,アスペリティと非地震性領域の棲み分けー室内実験と数値実験ー,地震学会予稿集秋季大会, P163, 2002. Yoshida. S., A. Kato, N. Kato, and M. Nakatani, Interpretation of various slip modes on a plate boundary based on laboratory and numerical experiments, Earth Planets Space, in press, 2004. |