Takeshi Akuhara1 , Michael G. Bostock2 , Alexandre P. Plourde2, and Masanao Shinohara1
1Earthquake Research Institute, The University of Tokyo, Tokyo, Japan, 2Earth, Ocean and Atmospheric Sciences, The
University of British Columbia, Vancouver, British Columbia, Canada
JGR: Solid Earth First published: 24 January 2019 https://doi.org/10.1029/2018JB016499
Abstract
Receiver functions, calculated by deconvolving P (or vertical) component records of teleseismic waveforms from the corresponding SV (or radial) components, have been widely used to obtain receiver‐side Green’s functions in an approximate form. Conventional receiver function methods, however, often fail due to numerical instability of the deconvolution and strong multiples on the P components. These problems become severe when analyzing in high frequency and using data from ocean bottom seismometers (OBSs).
We present a novel technique to estimate Green’s functions of receiver‐side structure from teleseismic P waveforms. In this method, two components of Green’s functions, which are assumed to form a series of pulses, are directly related in a single equation without explicit deconvolution. Based on the equation, we construct posterior probability distributions regarding the number of pulses, their timing, and amplitudes within a transdimensional Bayesian framework. A reversible‐jump Markov chain Monte Carlo method is used for this purpose, and we further utilize a parallel tempering method to achieve rapid convergence.
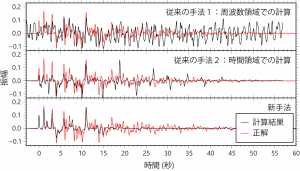
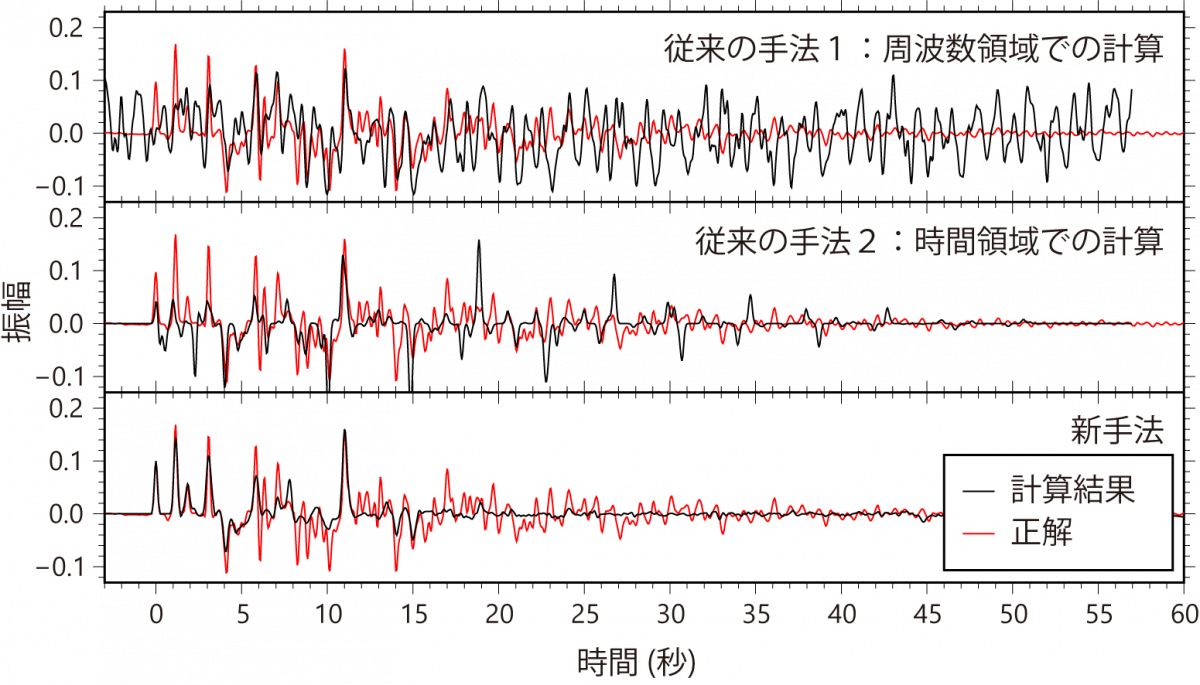
Synthetic tests and application to an OBS installed at the Yamato Basin, the Sea of Japan, show that the proposed method can estimate radial‐component Green’s functions more accurately than conventional receiver function methods. We suggest that the high‐frequency Green’s functions estimated by the new method can be used to reveal fine‐scale (in order ~100 m) structure of the seafloor sediment.