安崎遼路, 伊藤伸一, 長尾大道, 水牧仁一朗(高輝度光科学研究センター), 岡田真人(新領域創成科学研究科), 赤井一郎(熊本大学)
Phase prediction method for pattern formation in time-dependent Ginzburg-Landau dynamics for kinetic Ising model without a priori assumptions of domain patterns
Phys. Rev. B 103, 094408
DOI:10.1103/PhysRevB.103.094408
計算地球科学研究センターでは基礎的な研究活動の一環として、物質の中で起こる「相転移」という現象をコンピュータで再現することに取り組んでいます。相転移が起きると、物質の中のエネルギーなど、物理的な量が突然大きく変わり、外から観測できる部分にも大きな変化が現れることがあります。このような相転移には多くの場合、物質の「対称性」というものが関係しています。
相転移のことを研究する上で、一番簡単なモデルが磁石です。特に、回転しない磁石は強さを別にするとN極が上か、S極が上かのどちらかしかありません。そして、何もない空間に浮かんだ磁石にはN極とS極を入れ替えても全体のエネルギーは変わらない、という対称性があります。世の中にある磁石や磁石に反応する物質は実際にはたくさんの小さな磁石(スピンとも呼ばれます1)が集まった構造をしていますが、ひとつひとつスピンが隣のスピンや外からの刺激に対して反応することで、全体としての外からの刺激への応答が決まります。このような、磁石や磁石に反応する物質をまとめて磁性体と呼びます。
とても薄いある種の磁性体のフィルムに外から磁気的な刺激を与えたのちに刺激を取り去ると、フィルムの上に磁力の強い場所と弱い場所の模様ができることが知られています。この模様は、フィルムの厚みなどによって違うこともわかっていました。本研究におけるコンピュータシミュレーションによって、この模様には大きく分けて3種類あることがわかりました。これらの模様にはお互いに徐々に変わるのではなく、ある値を超えると突然次の模様に変わる、という性質があります。これは相転移の典型的な例です。また、研究の結果、これらの模様は空間の対称性とスピンの対称性(N極とS極を入れ替える)によって自然に分類されることもわかりました。
これらの模様のうちどれができるかは、実際にシミュレーションしないと分からないのでしょうか? 私たちはどの種類の模様ができるかを、対称性による相の分類を取り込んだ新しい方法を使って理論的に予測することに成功しました。 そうやって得られた理論的な結果は、実際にコンピュータでスピンを動かしてシミュレーションした結果ともほぼ合っていることが確かめられました。私たちは、この結果は磁石や岩石のような相転移を示す物質に対して、その物質の持っている見えないパラメータの値、例えば隣どうしのスピンの結びつきの強さ、を推定することに応用することを目指しています。将来的には、この手法は多くの成分からなる岩石などの系について、岩石の中の結晶や亀裂の成長の予測に使えるのではないかと期待しています。
注1. ここで言う「スピン」は電子の持つ内部自由度としてのスピンではなく、それらを粗視化した結果を指します。
注2. 運動方程式としては双極子間相互作用を入れた時間依存 Ginzburg-Landau 方程式を使っています。
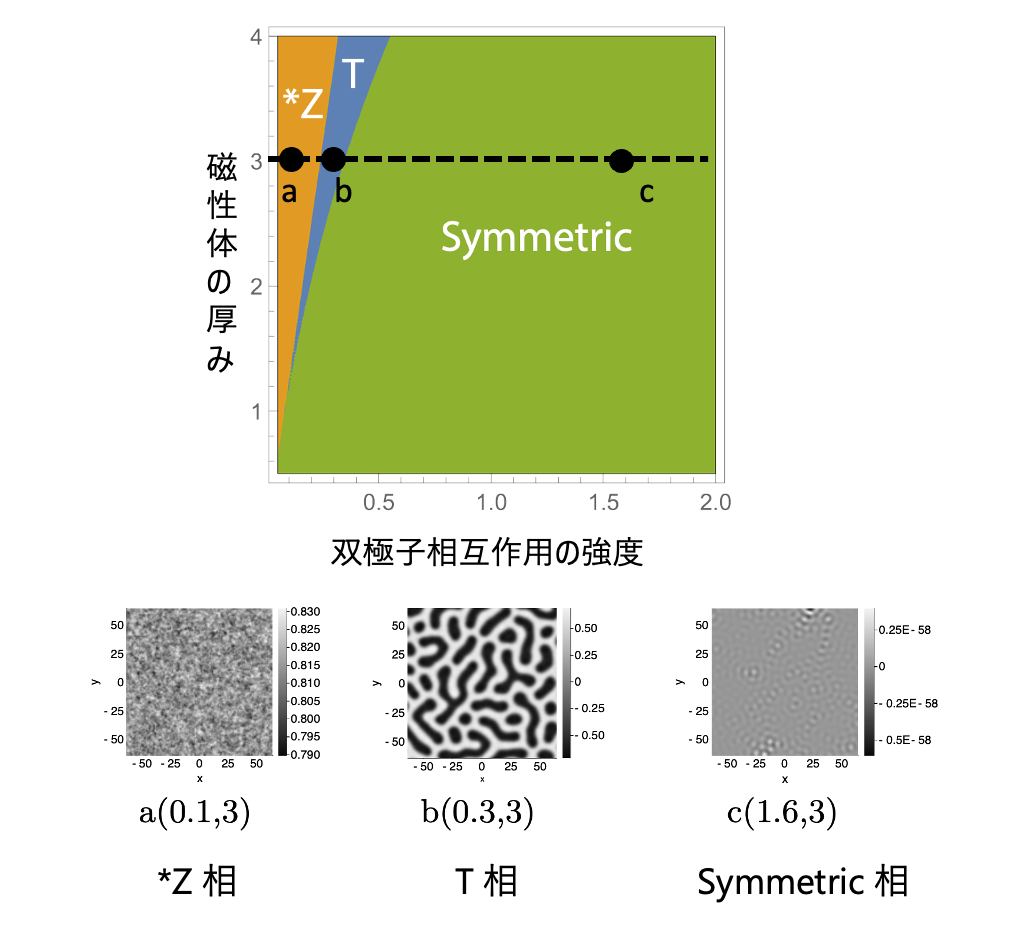
図.提案手法で描いた相図(上)と、その中の点 a, b, c での磁化の模様(下)。 相図の横軸(「双極子相互作用の強度」)はスピン同士が反対向きを向く傾向を、縦軸(「磁性体の厚み」)は磁性体フィルムの厚さを表しており、それらの値ごとに系の作る空間パターンが変わっているのがわかります。
謝辞 この研究は科学技術振興機構の戦略的創造研究推進事業CREST (JPMJCR1761, JPMJCR1861) によって支援されたものです。