【共同利用】平成30年度国際室外国人客員教員の推薦公募について
締切:平成29年8月18日(金)
詳細:公募要領
EGU2017での同窓会
4月23-28日にオーストリアのウィーンで開催された、EGU General Assembly 2017(欧州地球科学連合2017年大会)での展示ブースにて、これまで国際室の招聘制度を利用して地震研に滞在されたことのある共同研究者の方々との同窓会が開催されました。

当日は多くの懐かしい顔ぶれが訪れてくださり、旧交を温め情報交換をする良い機会となりました。
「国際室招聘制度」は、毎年公募がされ、海外の研究者を地震研に招聘し、国際共同研究の活性化を図る制度です。
詳しくは:http://www.eri.u-tokyo.ac.jp/kokusai/english/index.html
2017年の霧島山硫黄山火口周辺の火山活動
ウェブサイト立ち上げ:2017年5月11日
最終更新日:2017年5月15日
えびの高原では、硫黄山方向が隆起する傾斜変動が繰り返しみられており、気象庁が2017年5月9日に、噴火警戒レベルを1から2に上げています。
このページでは現地調査の報告を更新しております。
2017年5月15日
霧島山硫黄山噴気帯での熱異常域拡大に伴う噴気・噴湯孔の出現について
霧島山硫黄山火口の南側では,2017年3月頃から噴気・噴湯孔が出現するなど熱異常域の拡大が認められる.これらの出現位置や噴気活動の様子は,今後の硫黄山周辺の火山活動の推移を考える上で重要であると思われるので以下に報告する.なお,噴気孔Aの土砂噴出(5月11日火山噴火予知連委員会に報告)については,その後の気象庁カメラの画像解析から4月26日午前11時半頃と推定される.
1.硫黄山火口周辺の熱異常域の拡大について
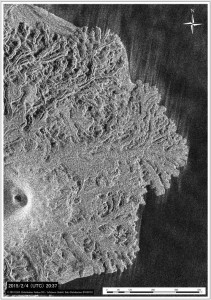
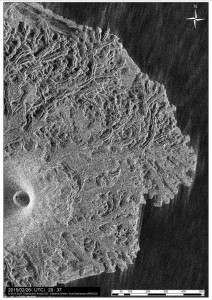
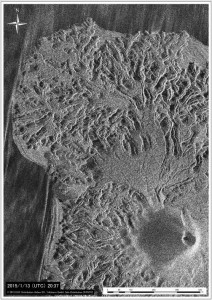
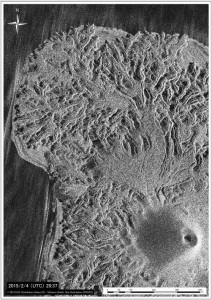
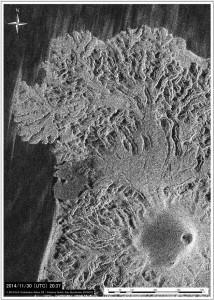
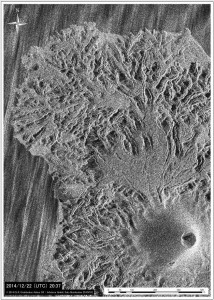
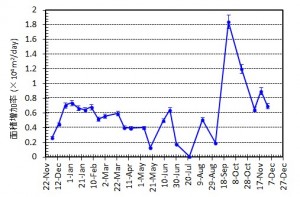
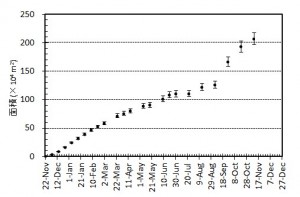
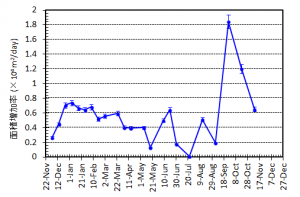
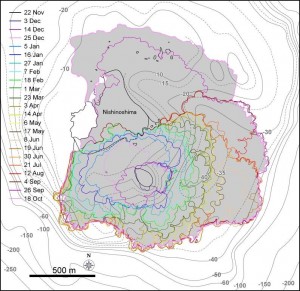
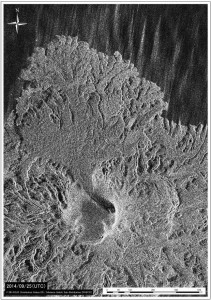
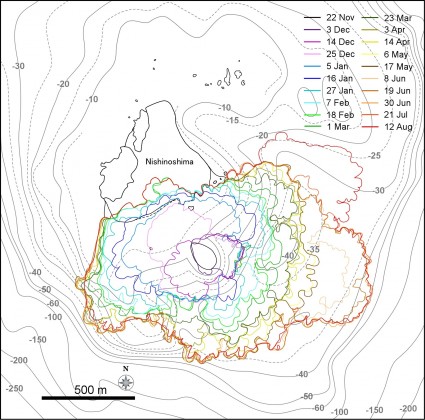
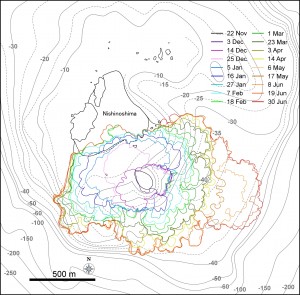
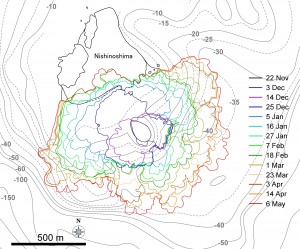
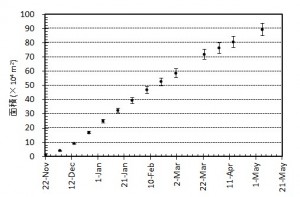
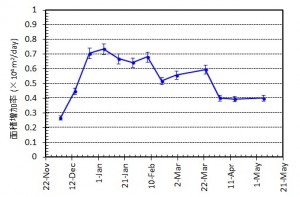
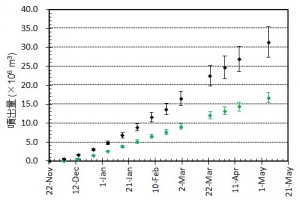
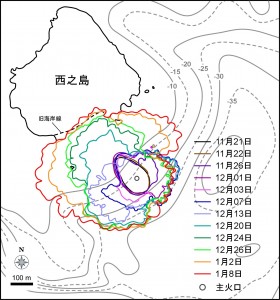
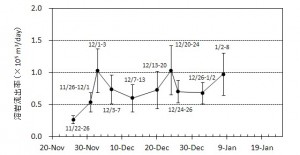
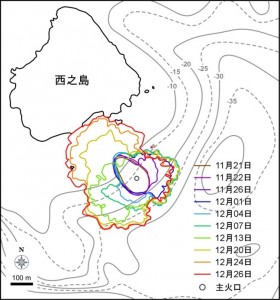
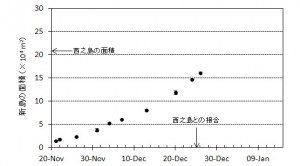
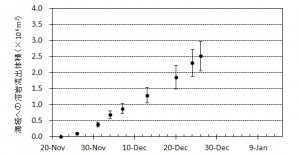
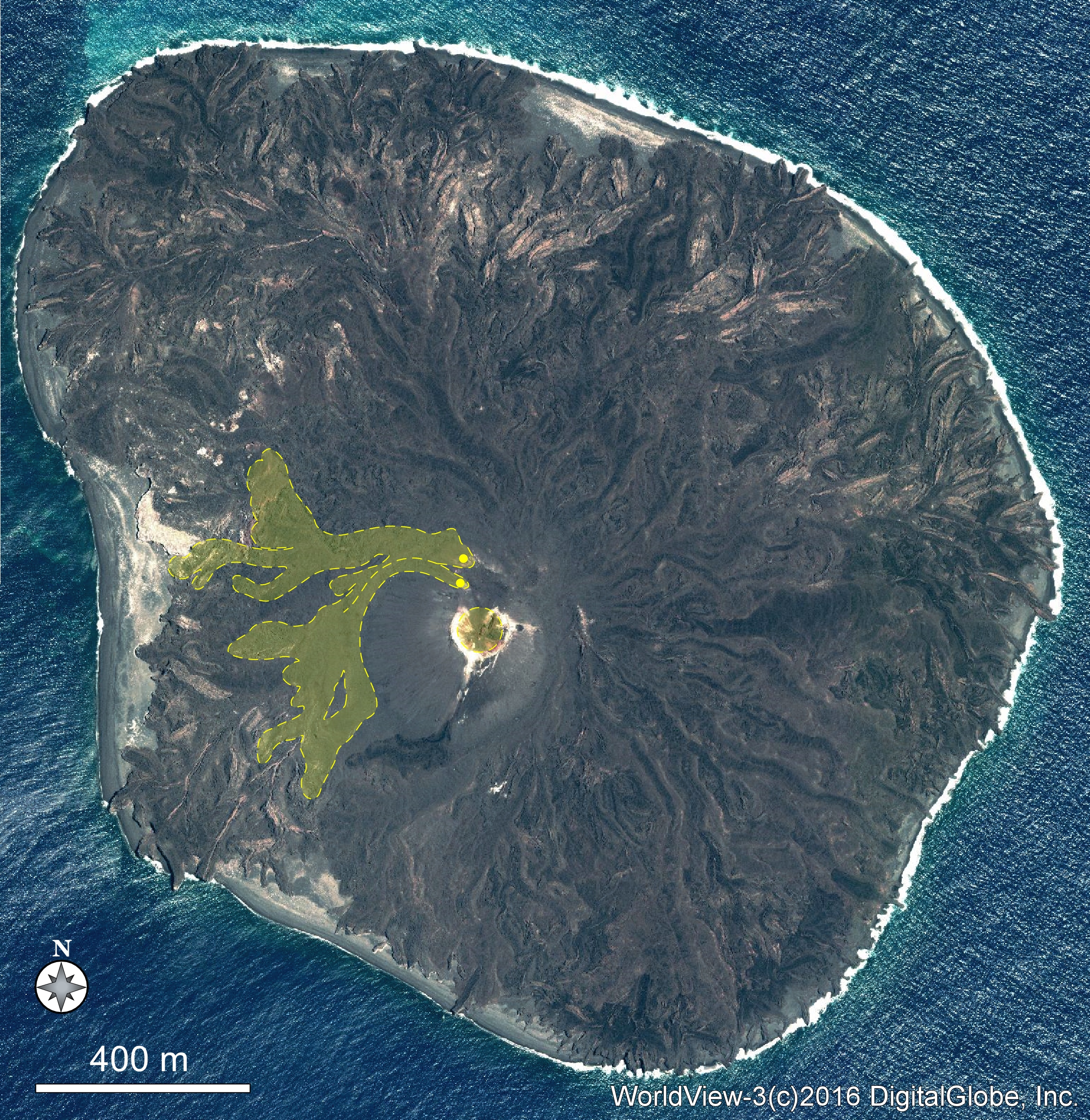
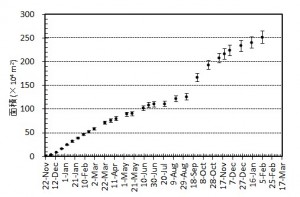
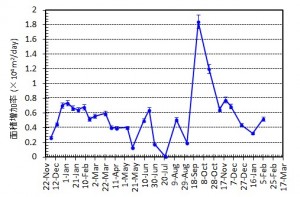
第137回火山噴火予知連絡会資料(その2の4 霧島山,p77)に報告したように,硫黄山火口南側及び硫黄山南斜面では熱異常域(硫黄山噴気帯: 舟崎・他,2017)が認められる.東京大学地震研究所等*では2017年3月19日に熱異常域を測定し,それ以前に続き熱異常域が拡大していることを確認した(図1).
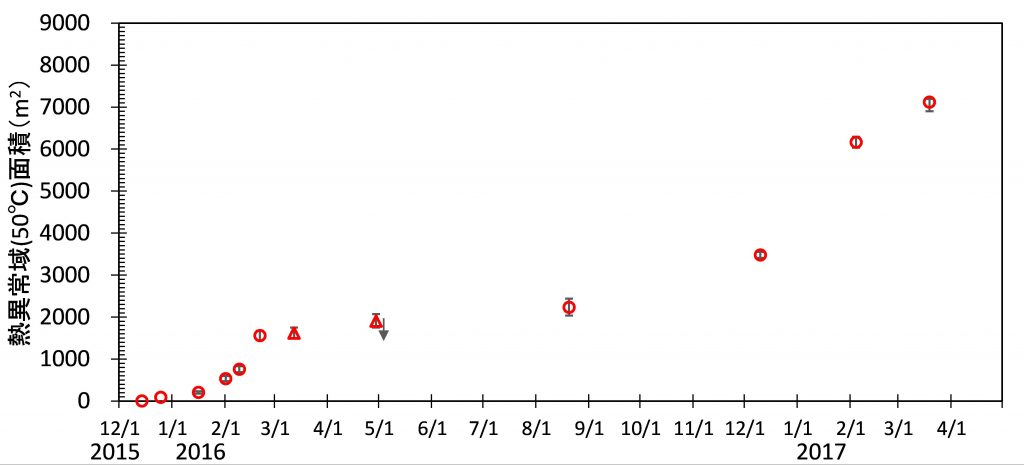
2016年1月16日~8月20日の簡易計測による面積測定誤差は±1 mを見込んだ.△は2016年2月21日の面積に,新たに生じた高温域の面積を追加した.
2. 硫黄山噴気帯の熱異常域拡大に伴う地表変状
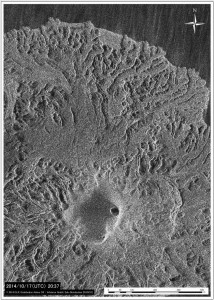
図2に硫黄山噴気帯の50℃以上の熱異常域(2017年3月19日観測)と,噴気・噴湯孔の位置を示す.地熱活動に伴い熱水や温泉が湧き出る現象を,ここではえびの高原自然保護対策協議会(1987),舟崎・他(2017)等に基づき噴湯とし,その孔を噴湯孔と呼ぶ.なお,図2に示した黄色の着色範囲は2017年5月5~10日の調査時に噴気量が多かった場所であり,これらを噴気域と呼ぶ.また,噴気域には径数10cm以上の円~方形の孔が形成され,そこから強い噴気が生じているものを噴気孔と呼ぶ.
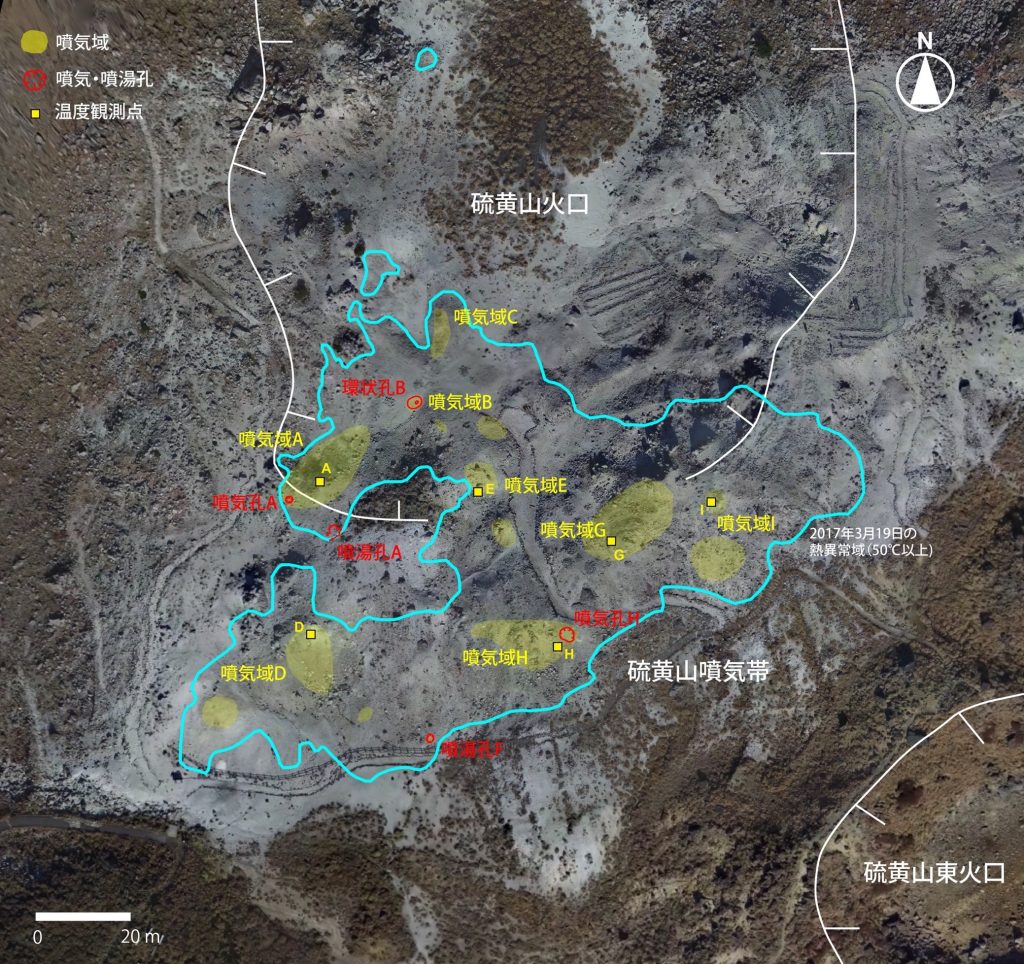
青線は2017年3月19日に観測した50℃の熱異常域.噴気域,噴気・噴湯孔は,5月5日~10日に確認した地点及び範囲を示している.硫黄山噴気帯は,舟崎・他(2017),硫黄山火口・硫黄山東火口は,田島・他(2014)による.
(1) 噴湯孔A
2017年3月19日に噴気域A周辺の熱異常域南端に,2箇所の噴湯孔(2m×1m,1m×0.5m)を確認し(噴湯孔A),それらから熱水(92.2℃)がわき出していた.その際2孔あった噴湯孔Aは4月22日には合体し1孔となり,5月7日には4m×3mに,10日にはさらに別孔が形成され複合孔となって5m×3mに拡大した(図3).噴湯孔Aは,2月4日に確認されていないので,2月4日~3月19日間に形成されたと考えられる.

矢印は噴湯孔を示す.A) 2孔の噴湯孔が見られ,写真上側孔は長辺2m,短辺1m,下側孔は長辺1m,短辺0.5m(2017年3月19日撮影). B) 噴湯孔Aの長辺4m,短辺3mであり周辺に泥のしぶきと思われる着色域が見られる(2017年5月7日撮影).
(2) 噴湯孔F
3月22日,噴気域Dと噴気域Hの中間南側に径約1mの噴湯孔Fが気象庁(2017:火山活動解説資料平成29年3月)によって確認された(図4).4月22日には噴湯孔Fは径約1.8mに拡大.3月19日に噴湯孔Fは確認されていないので,3月19日~3月22日間に形成されたと考えられる.

噴湯孔は直径1.8m,深さ50cm(2017年4月22日撮影).
(3) 噴気孔H
2017年4月22日に径約1.5mの噴気孔Hが確認され,そこから轟音を伴う強い噴気が噴出していた(図5).写真比較により,噴気孔Hの周辺には径1m程の岩塊が新たに堆積していることを確認.4月22日には,噴気孔周辺に泥の付着も確認(図6B).従って,噴気孔Hの形成時には地表の岩塊が飛ばされ周辺に落下し,同時に泥が混入した熱水が噴出したと考えられる.さらに,5月5日には,噴気孔Hの拡大と孔周辺に数cm大の礫の堆積しているのが認められた(図6C).噴気孔Hでは礫を放出しながら拡大していると考えられる.

矢印は噴気孔Hの位置を示す.A) 噴気域Hの噴気状況(2017年2月4日撮影). B) 噴気域Hの噴気量がやや増す(2017年3月19日撮影).C) 噴気域H内に,噴気孔Hが形成され強い噴気が生じる(2017年4月22日撮影).D) 噴気孔Hから強い噴気が放出される(2017年5月5日撮影).

イタリック英字は同じ岩石を示す.A) 噴気孔H形成以前の地表状況(2016年11月5日撮影). B) 噴気孔H形成後の地表状況.直径約1.5mの噴気孔が形成され,孔の下方に岩塊が堆積している.孔の上方には泥の付着も認められる(2017年4月22日撮影).C) 噴気孔Hの拡大状況.岩石aが拡大した噴気孔の中に取り込まれる.岩石aとfの間に礫の堆積が認められる(2017年5月5日撮影).
(4) 噴気孔A
噴気孔Aは噴気域Aの南西端に形成され,形成に伴って土砂及び火山灰を放出した.前回報告ではヒアリングを元に4月28日~5月5日の間に形成されたとしたが,気象庁の霧島山(硫黄山南)カメラ(以下,硫黄山南カメラ)の画像から4月26日にこの土砂噴出が生じていたと推定される.
すなわち,硫黄山南カメラ画像によれば4月26日朝までは噴気域Aからの強い噴気は見られない.しかし,26日午前11時29分画像には噴気域A付近から,薄灰白色(薄い着色)の水蒸気プリュームが立ち上る様子を確認できる(図7).また,午前10時20分,11時7分にも薄い着色した白色噴気が見られる.午前10時20分~11時30分頃の噴気は南西向きに流れており,先に報告した火山灰の付着域の分布と一致する.噴気孔A周辺では土砂が北東側に拡がって堆積しているので,午前11時29分頃にサーマル雲が北東まで拡がり,その時に土砂が噴出したと推定される.

(http://www.data.jma.go.jp/svd/volcam/data/volc_img.php)
(5) 環状孔B
上記の噴気・噴湯孔の出現以外に,5月7日噴気域B付近において最大径2m以上の環状キレツが形成(環状孔B)を確認した.環状孔Bの中心には,深さ10~20cm程の陥没が5月7日に生じており,その後,陥没はさらに進行した。

最大直径2m以上の環状キレツが形成され,複数のキレツから噴気が生じている(2017年5月7日撮影)
引用文献
- えびの高原自然保護対策協議会 (1987) 環境庁委託業務報告書 霧島屋久国立公園えびの高原地区における事故防止対策のための検討調査報告書,28-40.
- 舟崎淳・下村雅直・黒木親敏 (2017) 霧島連山えびの高原,硫黄山の明治時代以降の地熱活動資料. 験震時報, 80, 1-11.
- 気象庁 (2017) 霧島山の火山活動解説資料(平成29年3月). 1-28. http://www.jma-net.go.jp/fukuoka/
- 田島靖久・松尾雄一・庄司達弥・小林哲夫 (2014) 霧島火山えびの高原周辺における最近15000年間の活動史. 火山,59,55-75.
(* 図・写真等は田島靖久氏による)
(火山噴火予知研究センター 中田 節也)
2017年5月10日
2017年5月10日の霧島山硫黄山噴気地帯の動画:

(撮影:中田節也)
2017年5月11日
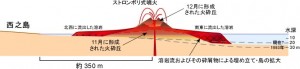
霧島山硫黄山火口周辺で発生した土砂噴出について
硫黄山火口の南側では,2017年3月19日,21日に2地点の噴湯孔,4月22日に轟音を伴う噴気孔の出現を確認するなど火山活動が活発化している.東京大学地震研究所及び霧島ネイチャーガイドクラブ等*が,5月5~10日に現地調査を実施し,硫黄山火口の南西縁において土砂噴出を伴う新たな噴気孔を確認したので,その結果を報告する.
- 硫黄山火口の南西縁での土砂噴出
新たに確認した噴気孔(以下,噴気孔A)は硫黄山火口の南西縁にあり,第137回火山噴火予知連絡会資料(その2の4霧島山,p78)に報告したB点付近に形成された.噴気孔Aは,深さ1m以上,長さが約1.5m四方の方形であり(図3),そこから強い噴気が放出されていた.本噴気孔は,4月22日に調査した際には生じておらず,地元での聞き取りからは4月28日~5月5日の間に出現したものと考えられる.
・噴気孔Aの周辺には土砂噴出物が認められ,土砂噴出物は噴気孔から北東及び南西方向に分布する.土砂噴出物に覆われた地表は暗灰色を呈する(図1,2).
・南西方向では,シルト質火山灰の付着によって地表が灰白色化しており,さらに延長方向では緑色葉上や岩の窪みなどに灰白色のシルト質火山灰が付着や沈殿しており,その痕跡は噴気孔Aから距離にして約200mまで追跡できる(図1).
・噴出物は上下2層からなり,下位は砂質火山灰,上位はシルト質火山灰である(図4)
・噴気孔A周辺の2ヶ所から採取した噴出物量は,それぞれ3.8 kg/m2,3.4 kg/m2であった(図1).噴出物は,噴気孔周囲の暗灰色の変色範囲をほぼ一様の厚さで覆っていると仮定し,2ヶ所の噴出物量の平均値と暗灰色域面積より,噴出物量は約1トンと概算される.
噴気孔A周辺に堆積した噴出物量は,その孔の大きさから推定される欠損量とほぼ一致する.噴出物の上位層が灰白色のシルト質火山灰であることは,先に噴気孔拡大が起こり,その後,泥を含む熱水が噴出したと考えられる.南西に拡がった火山灰の分布は,灰白色のシルト質火山灰から構成されており,泥を含む熱水の飛沫が強い風によって拡散することによって生じたと考えられる.本現象は,地表下のごく浅い所にある熱水溜まりの圧力が高まり地表を破砕し生じた土砂噴出と推定される.
(* 図面作成等は田島靖久氏による)
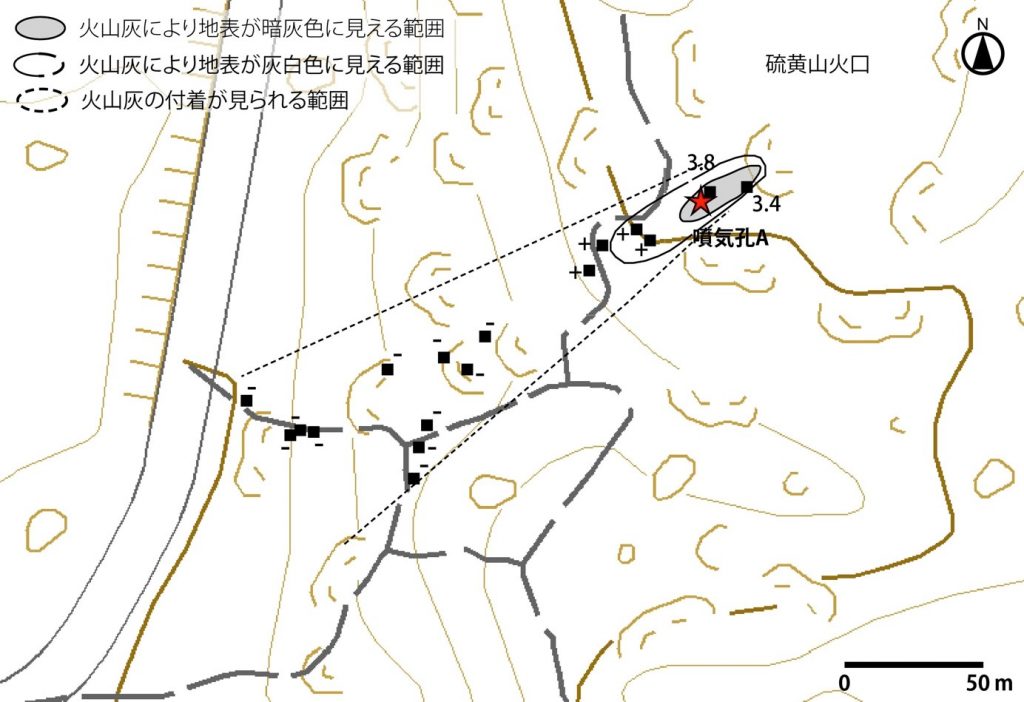
四角は観測箇所.数値:堆積物量(kg/m2),+:堆積物あり,-:堆積物がわずかに認められる.
背景地図は国土地理院地図(電子国土WEB).左に県道1号線が南北に走る.


孔の縁には噴き上げられた土砂の高まりができている

下位は砂質火山灰,上位はシルト質火山灰によって構成される.
(火山噴火予知研究センター 中田 節也)
【受賞】川勝均教授がBeno Gutenberg Medalを受賞
川勝均教授が、Beno Gutenberg Medalを受賞しました。授賞式はEGU General Assembly 2017(欧州地球科学連合2017年大会)の会期中に開催され、1時間のレクチャーがされました。
*Beno Gutenberg Medalは、地震学に多大なる貢献をした人物に対し、EGU(欧州地球科学連合)の地震学部門より与えられる賞です。
EGU(European Geoscience Union) website: Beno Gutenberg Medal

2017年4月18日からの西之島の噴火活動
2017年4月18日からの西之島の噴火活動について、「地震火山情報」の「西之島の噴火活動」ページにて情報が公開されております。随時更新がされております。
地震火山情報:西之島の噴火活動
2013年11月21日西之島の噴火活動
ウェブサイト立ち上げ:2013年11月21日
最終更新日:2017年4月28日
2017年4月18日に再び噴火があり、このページで情報を随時更新しております。
2013年11月21日小笠原諸島の西之島周辺で噴火活動が起きました。
西之島2017年噴火による溶岩流の分布と推定される噴出率(続報) (前野深)
西之島の噴火活動(2017年4月25日上空観察) (前野深)
西之島2017年噴火による溶岩流の分布と推定される噴出率 (前野深)
ひまわり8号AHI画像による西之島の活動再活発化の検出(金子隆之)
西之島の噴火活動 2017年4月21日上空観察(中田節也)
2017年4月18日からの西之島の噴火活動について(武尾実)
2016年11月7日西之島調査の動画を公開
2016年10月26日西之島調査の概要について
2016年10月11日【プレスリリース】小笠原諸島西之島の火山成長過程と生物相成立過程の調査を開始
2015年7月15日「なつしま」から観察した西之島の噴火活動状況(前野深)
2015年3月15日西之島における噴火活動について[続報](前野深)
2015年3月4日西之島の火山活動(中田節也)
2015年2月5日までの西之島噴火活動について[続報](前野深)
2014年12月23日までの西之島噴火活動について[続報](前野深)
2014年12月14日西之島における噴火活動について[続報](前野深)
2014年12月3日西之島火山の活動–父島での空振モニタリングで判明(市原美恵・西田究)
2014年11月20日西之島における噴火活動について[続報](前野深)
2014年11月13日西之島の噴火活動(観察者:中田節也)
2014年10月24日西之島における噴火活動について[続報](前野深)
2014年9月5日西之島における噴火活動について[続報](前野深)
2014年8月18日西之島における噴火活動について[続報](前野深)
2014年7月14日父島で捉えた西之島火山の活動に伴う空振(市原美恵)
2014年7月8日西之島における噴火活動について[続報]前野深)
2014年5月27日西之島における噴火活動について[続報](前野深)
2014年1月16日西之島における噴火活動について[続報](前野深)
2014年01月10日西之島における噴火活動について(前野深)
2013年12月26日12:30-13:00西ノ島の火山活動(観察者:中田節也)
2013年12月25日西之島2013年活動の航空機観察(観察者:金子隆之)
2013年12月24日新島成長過程[続報](観察者: 前野 深)
2013年12月20日12:20-13:05上空観察(観察者: 前野 深)
2013年12月17日新島成長過程[続報](前野 深)
2013年12月13日 新島成長過程(前野 深)
2013年11月24日午前11:20-12:05 上空観察(観察者:中田節也)
2013年11月21日9時13分~31分 上空観察(観察者:金子隆之)
2017年4月28日
西之島2017年噴火による溶岩流の分布と推定される噴出率(続報)
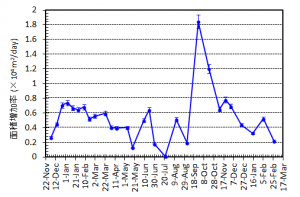
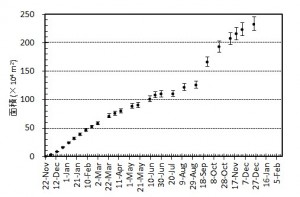
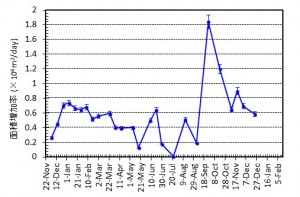
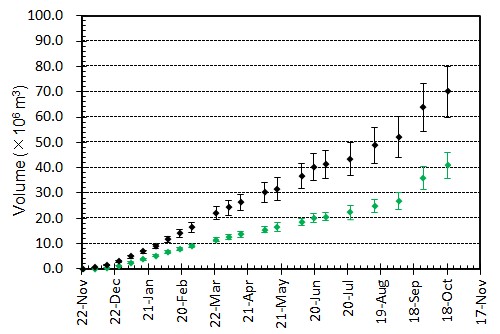
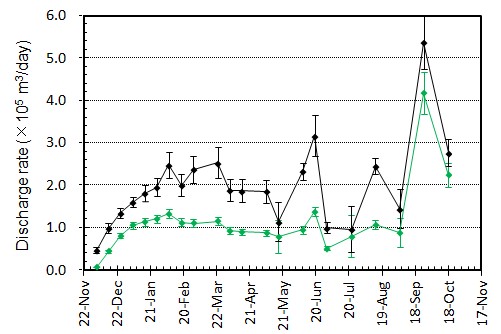
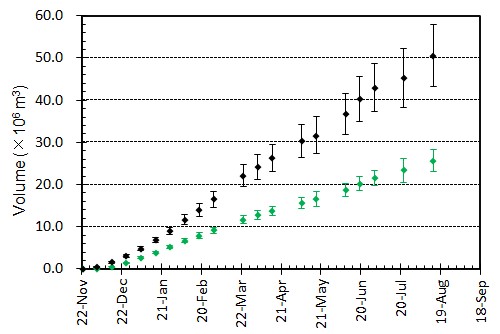
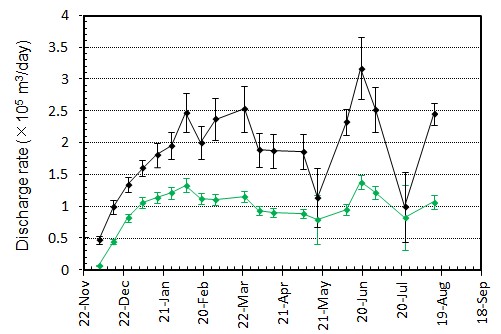
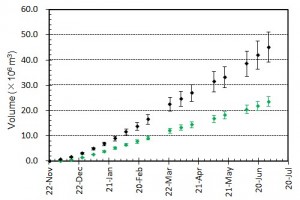
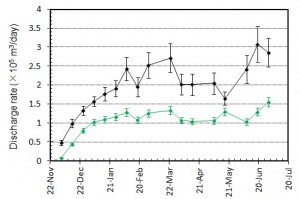
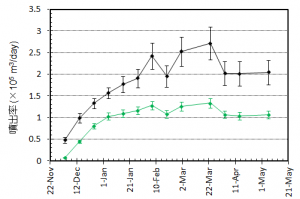
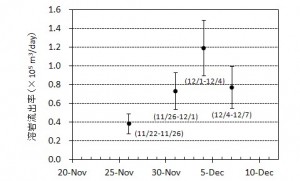
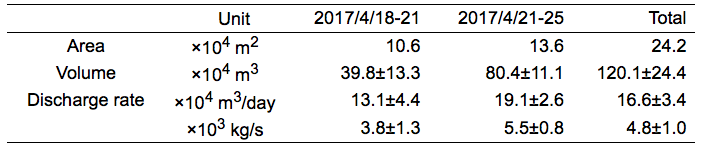
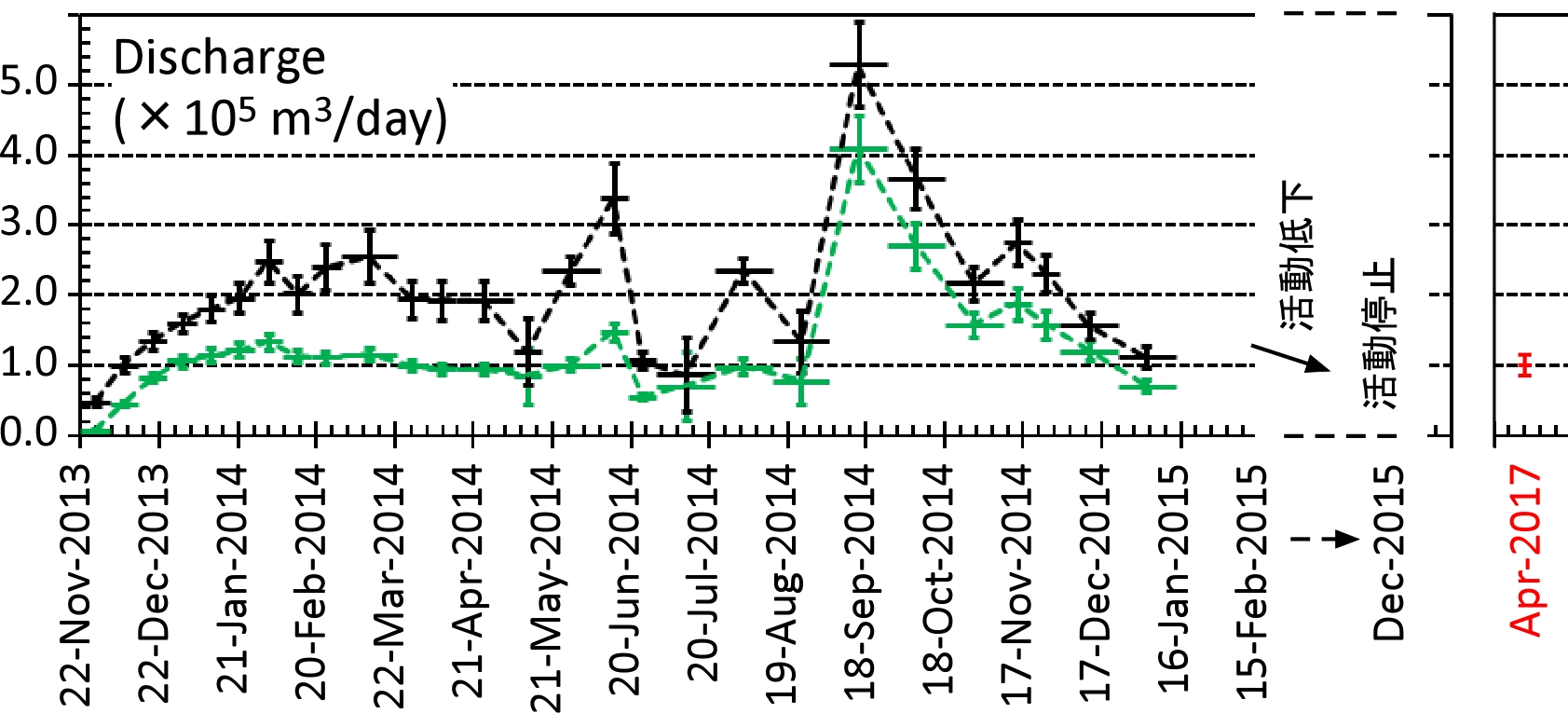
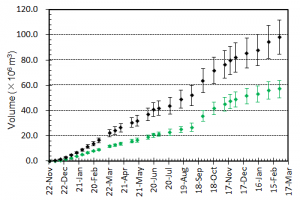
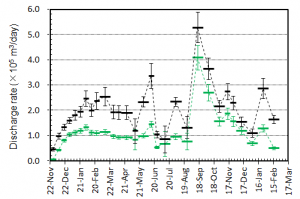
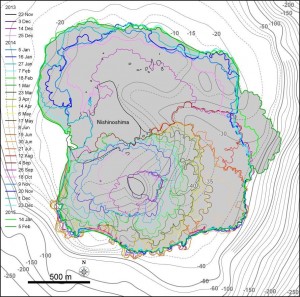
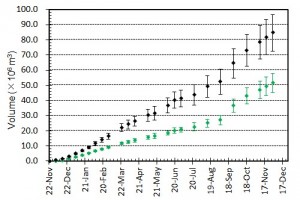
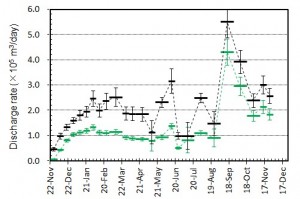
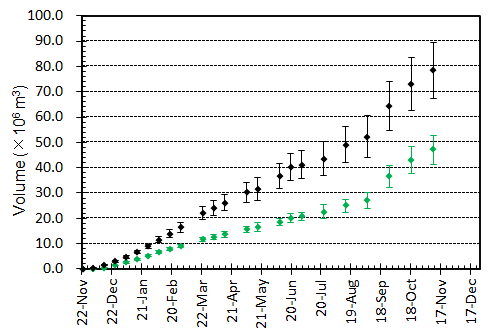
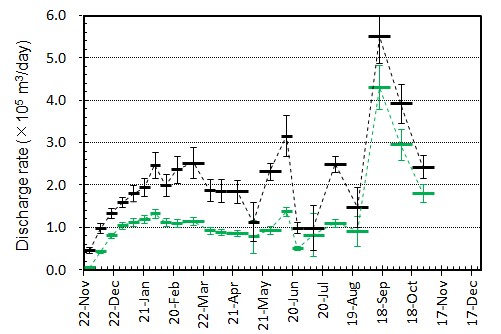
概要: 西之島の噴火により流出した溶岩の分布,体積,噴出率について,4月25日に実施した上空からの観察結果1)をもとに解析した。溶岩流はスコリア丘北側の3ヶ所の火口から西側に向けて流出し,低所を埋めながら海岸に向けて流れている(図1)。分布面積はおよそ24万m2(火口を除く)である。4月21日の観察結果2)も含めたこれまでの面積,体積,噴出率の推移はTable 1のようになる。なお,溶岩による地形の被覆状況から,内陸部での溶岩の厚さは平均2.5-5 m,海岸に流出した部分については平均10 mと仮定している。これらの値には大きな誤差が含まれている可能性があるが,それを考慮したとしても流出した溶岩の総体積はすでに約100万m3に達していると考えられる。4月21日から25日までの4日間の平均噴出率は,21日までの3日間の噴出率よりやや増加し,およそ19万m3/day(5-6トン/秒)と推定される。この値は2013-2015年噴火時の平均噴出率と同程度である(図2)。噴出率の変化は活動推移を予測する上で重要であり,今後注視していく必要がある。
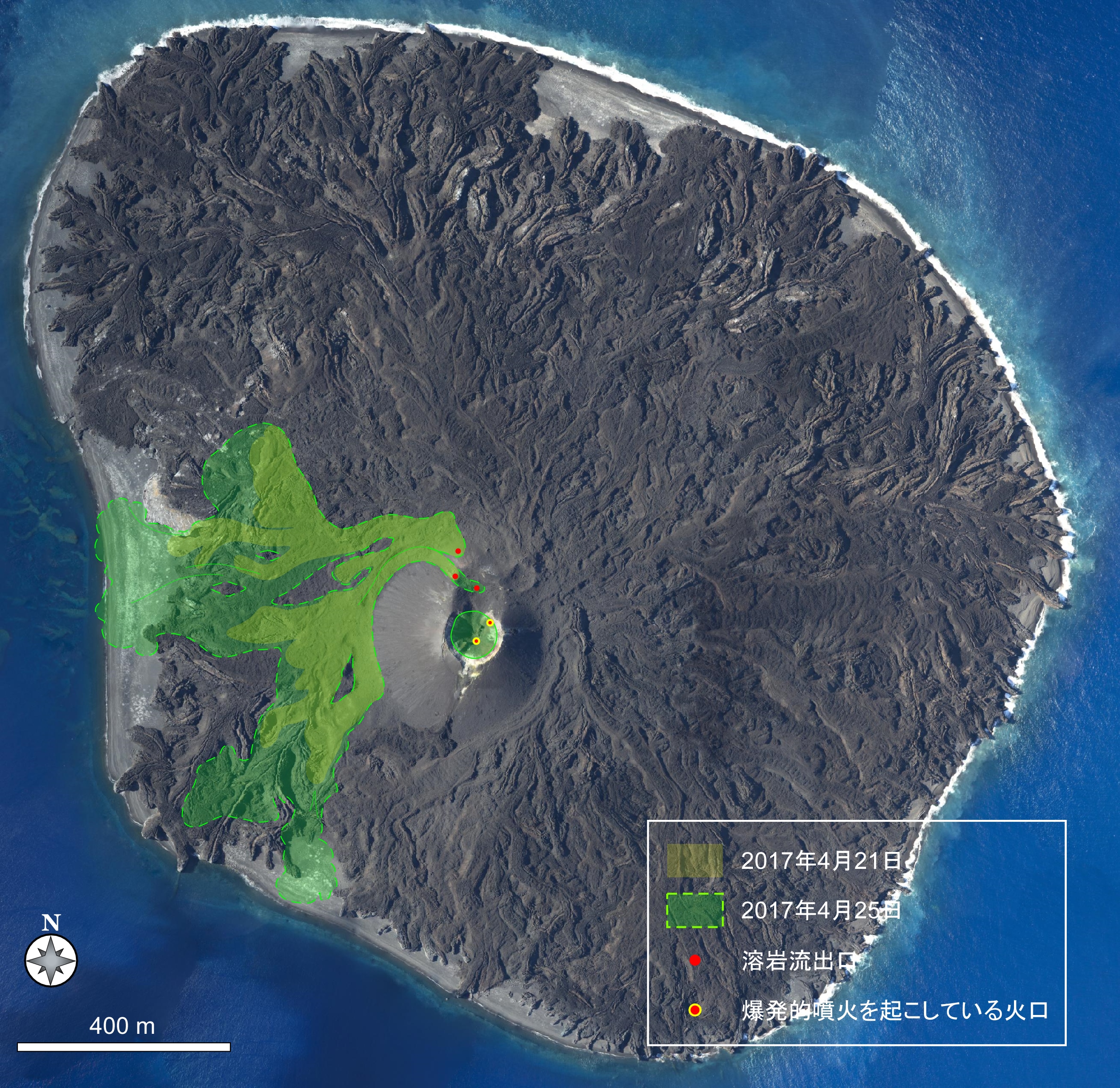
- 火山噴火予知連絡会資料 西之島の噴火活動(2017年4月25日上空観察)(2017年4月25日)(東大震研)
- 火山噴火予知連絡会資料 西之島の噴火活動(2017年4月21日上空観察)(2017年4月21日)(東大震研)
- 国土地理院による西之島の噴火活動関連情報のHP: http://www.gsi.go.jp/gyoumu/gyoumu41000.html
(2017年4月28日火山噴火予知研究センター前野)
2017年4月26日
※報道関係の方へ: 写真の引用は,読売新聞社にお伺いください。
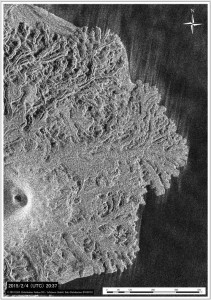
概要: 西之島の噴火活動を上空より観察した(読売新聞社の協力による)。観察日時は,4月25日13:55-14:25のおよそ30分間である。スコリア丘山頂に2つの小火口,北側山腹・山麓に3つの溶岩流出口が存在し,新たな溶岩流は西之島の西側を広く覆っている(写真1)。
スコリア丘山頂の小火口のうち南側のものは活発で,ストロンボリ式噴火を繰り返し発生している(写真2)。数秒~数10秒ごとに灰褐色噴煙と共に火山弾を激しく噴出し,弾道を描いて飛散するものの中には長径数mを超えるものも含まれる。一方,山頂北側にも小火口が存在するが,こちらは不活発であり,灰色噴煙を伴う爆発が観察中に一回観測されたのみである(写真3)。噴火前のスコリア丘山頂のすり鉢状火口は,今回の活動による噴出物でほぼ埋まり,火砕物が降り積もることにより小火砕丘を形成し高度を増している。
溶岩流はスコリア丘北側山腹・山麓に形成された3箇所の溶岩流出口(このうち山麓に近い2箇所は21日に観察された流出口1)から西側に向けて流出し(写真3),2014-2015年に噴出した溶岩を広く覆っている。西側では溶岩先端は海に達している。幅およそ200 mに渡り西海岸を横切り海に流入し,水蒸気を上げて前進している(写真4)。旧島は新たな溶岩と接し,一部は新たな溶岩に覆われているものの大部分は残存している。溶岩流は南西側でも先端が海岸付近まで達し,海に向かい進んでいる(写真5)。
ストロンボリ式噴火は継続し,山頂すり鉢状火口は埋まりさらに高度を増しつつある。また,山麓・山腹からの溶岩流出は継続し,その流域面積は22日より大きく拡大していると考えられる。これらのことから,西之島の活動はこの4日間で衰えておらず,活発な状態にあるといえる。





- 火山噴火予知連絡会資料 西之島の噴火活動(2017年4月21日上空観察)(2017年4月21日)(東大震研)
(2017年4月26日火山噴火予知研究センター前野)
2017年4月22日
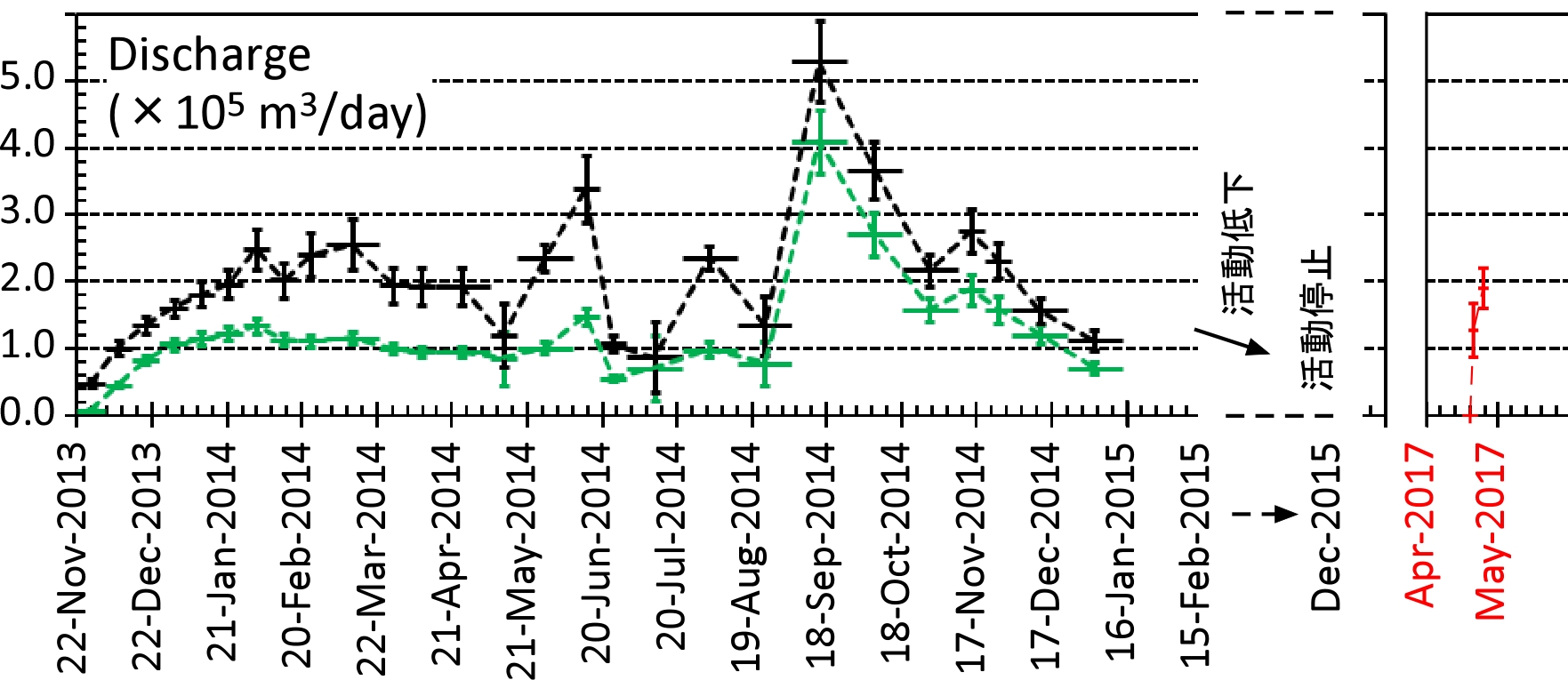
概要: 西之島で再開した噴火により流出した溶岩の分布,体積,噴出率について,21日に実施した上空からの観察結果1)をもとに解析した。溶岩流はスコリア丘北側の2ヶ所の火口から西側に向けて流出し,低所を埋めるように流れている(図1)。その分布面積はおよそ10万m2(火口を除く)である。溶岩による地形の被覆状況から,溶岩は高い流動性を有しており,層厚はせいぜい平均2-4 m 程度と考えられる。したがって流出した溶岩の体積は20-40万m3と推定される。流出の開始を地震活動が活発化した18日8時頃2)と仮定すると,およそ3日間の平均噴出率は約10万m3/day となる。この値は,2013-2015年噴火時の活動初期や2014年の低調な頃と同程度の噴出率である(図2)。噴出率の変化は活動推移を予測する上で重要であり,今後注視していく必要がある。
- 火山噴火予知連絡会資料 西之島の噴火活動(2017年4月21日上空観察)(2017年4月21日)(東大震研)
- 火山噴火予知連絡会資料 2017年4月18日からの西之島の噴火活動について(2017年4月21日)(東大震研)
(2017年4月22日火山噴火予知研究センター前野)
2017年4月21日
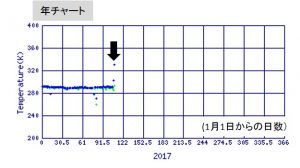
ひまわり8号 Advanced Himawari Imager(AHI)画像によって,西之島の活動再活発化が捉えられました(図1).ひまわり8号は全球を10分毎という高頻度で観測することができます.
4月17日2時50分UTC (日本時間17日11時50分)に,最初の熱異常が認められ(図2の矢印),この頃噴火が始まったと推定されます.4月19日の7時00分UTC (日本時間19日16時00分)頃から熱異常が増加し(図3の矢印.3.9 umのチャンネルで顕著に見えます),現在も高い状態が続いています(図4).(4月20日15時40分現在)

2017年04月17 日- 02:50 UTC(幅は約200 ㎞)

(幅は約200 ㎞)
(2017年4月20日火山噴火予知研究センター金子)
2017年4月21日
※ 報道関係の方へ:写真の引用については,朝日新聞社にお伺いください.
2017年4月18日頃に噴火活動を再開したと考えられる西之島において、上空観察を4月21日午前中実施した。西之島では、活発な噴火活動が継続しており、島中央部にある火砕丘付近から二つの溶岩が流下しているのが確認され、溶岩流は流域面積を拡大していた。
観察結果は以下のように要約される。
1.火砕丘の頂部にある火口は新しい溶岩と思われる噴出物で満たされていた。
2.火砕丘の中央北寄りの複数箇所から火山灰噴煙が数十秒おきに立ち上り、火山弾が上空約100m程度に噴き上がっていた。これらの噴火地点を中心として黒っぽく盛り上がり、新たに低い火砕丘が形成されているように見える。
3.元の火砕丘の上斜面北西側に、溶岩の流出口が位置しており、赤熱と青白いガスの放出が認められた。溶岩は斜面を下って、火砕丘の西側裾野を巻いて移動し、さらに南側に流れて扇状に広がっていた。
4.また、火砕丘の北側裾野には別の溶岩流出口があり、そこでも盛んに青白いガス放出を伴って赤熱が見られた。溶岩はそこから西に流れながら途中で複数に分岐し、一部は旧島の脇を通って海岸砂浜に達していた。
観測日時:2017年4月21日(金)午前9時15分〜9時40分
使用航空機:朝日新聞社機あすか



謝辞:観測の機会を与えていただいた朝日新聞社には感謝します。
(火山噴火予知研究センター:中田節也)
2017年4月21日
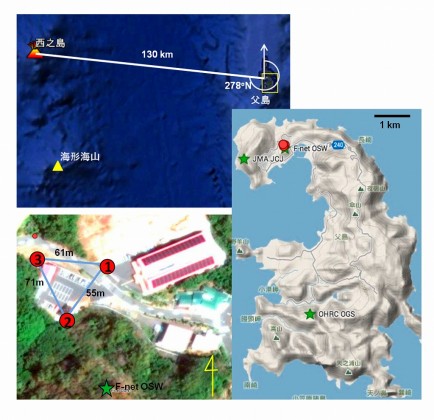
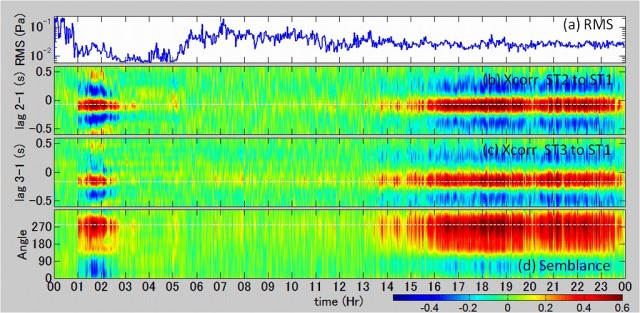
海上保安庁による上空からの観測で,4月20日14時過ぎに西之島の噴火が確認されたが,地震研究所が昨年10月に西之島の旧島に設置した地震・空振観測データから,この噴火に至る活動の推移を調査した.その結果を以下にまとめる.
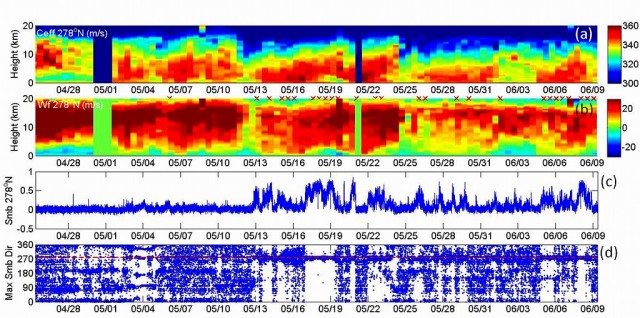
図1は西之島の観測点から伝送されてくる地震記録のスペクトログラムの4月1日〜19日までのデータを示している.4月17日11時頃から一群の震幅の大きなシグナルが発生し始め,次第にその頻度が増大していく様子が確認できる(赤丸で囲った部分 ).この活動はそれ以前には見られない活動である.さらに,18日8時頃から連続的続くシグナルが確認でき,それは19日も一日中継続している.

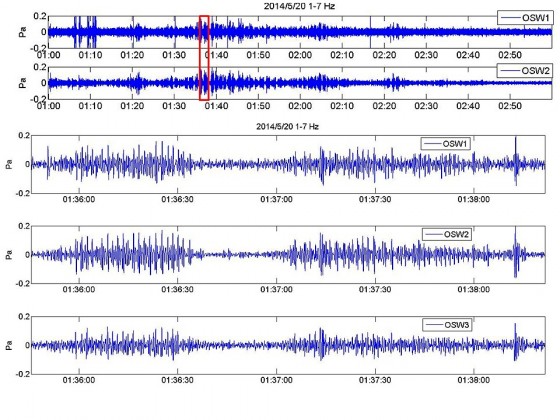
そこで,4月17日〜18日の地震・空振データをダウンロードして,これらのシグナルの実態を確認した.図2及び図3に4月17日と18日のそれぞれ一日分の地震記録と空振記録を示す.17日6時過ぎに高周波の地震の一群が発生し,その後,11時頃から低周波の相似地震の一群が発生し始めた(図2).
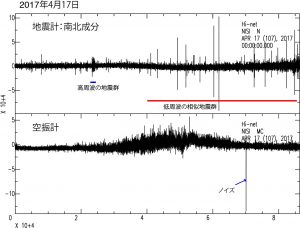
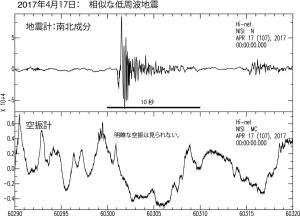
この17日に発生した相似地震と空振記録を図4に示す.この低周波相似地震に伴った空振は確認できないので,これらの活動には噴火が伴っていなかったと考えられる.この相似な低周波地震の発生頻度は18日に向けて徐々に増大し,18日に入ると頻発するようになる(図3).
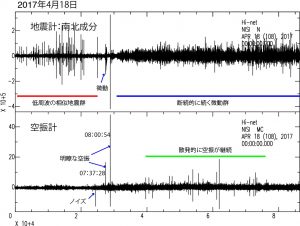
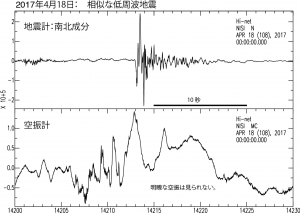
18日の相似地震と空振記録の例を図5に示す.18日の時点でも,この活動に伴う空振は確認できなかった.このような低周波の相似地震群の発生は,2011年新燃岳噴火のマグマ湧出期にも確認されており,その後の推移と合わせて判断すると,この時期に火道内部をマグマが上昇,充填したのではないかと推定される.ひまわり画像による最初の微弱な熱異常は17日11時50分頃に確 認されており,低周波地震の発生とほぼ一致していることも上の 推定を示唆する.
 |
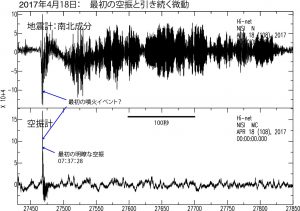
 |
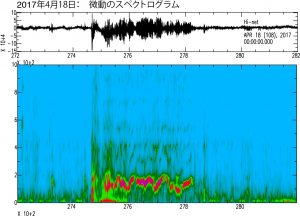
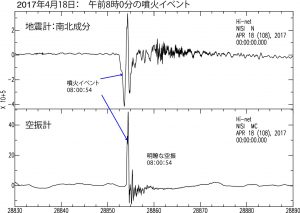
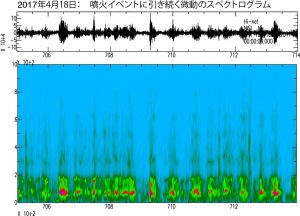
その後,7時37分には最初の明瞭な空振が観測され,それに引き続く形で微動が発生している(図6).この空振の振幅は17Paあり,これが最初の噴火イベントではないかと考えられる.微動は1Hzから2Hzの間に卓越周波数を持ち,その卓越周波数が短時間の間に大きく遷移する特徴を持っている.この微動のスペクトログラムを図7に示す.この微動が収まった6分後の8時0分に約48Paの空振を伴う噴火イベントが発生した.このときの地震と空振記録を図8に示す.この噴火イベントの後,図9に示すような断続的な微動波群がほぼ連続して発生し続ける状態に遷移した.この活動は19日まで継続しており,この時期に溶岩流が火口から溢れ出たのではないかと推察される.
 |
 |
(火山噴火予知研究センター:武尾実)
火山噴火予知研究センターのHPでも情報を更新しています。
火山噴火予知研究センター: 2013-2014年西之島の噴火について【最終更新日:2014年8月17日】
2015年7月15日
(火山噴火予知研究センター:前野深)
概要:
2015年6月11〜21日に実施されたJAMSTEC研究船「なつしま」による研究航海(NT15-E2*)中,船上から西之島の噴火活動状況について観察した.西之島は中央スコリア丘でストロンボリ式噴火を数10秒〜1分程度の間隔で継続するとともに,溶岩流がスコリア丘東山腹に形成された小火口丘の麓から流出し,島の南東端で海に達して島を拡大し続けている.噴煙下を航行した際には,船上に降灰が認められた.火山灰は,さまざまな形態を有する新鮮な黒色~褐色ガラスにより構成され,ストロンボリ式噴火を引き起こしている低粘性のマグマに由来するものである.西之島の噴火活動は依然として活発な状況にある.
* 研究の概要については下記ホームページを参照:
「海洋調査船による西之島および周辺海域の学術調査研究~海底面の撮影や地形調査、試料の採取、西之島火山の観察などを実施~(http://www.jamstec.go.jp/j/about/press_release/20150715/)
西之島の状況:
「なつしま」は西之島から4.5 km以上離れた海域に6月13〜18日の期間滞在した.その間,深海探査機ディープ・トウを用いた海底地質調査および試料採取を行い,ディープ・トウ潜航の合間に船上から西之島を観察した.調査期間中,ストロンボリ式噴火と溶岩流出は絶えることなく,マグマ供給は依然として継続していることが確認された.船の位置,同じ位置から撮影した島の形状,島の輪郭(5月に海上保安庁が報告)をもとに中央火口丘の標高を見積もったところ,140-150 m程度であった.このことから,国土地理院により標高137 mと計測された3月1日以降,中央火口丘はやや高くなったと考えられる.溶岩流はスコリア丘東山腹に形成された小火口丘(標高約100 m)の麓から南方向に流出し,緩斜面を形成して海に達し,島を拡大し続けている.活動的な中央〜南東域を除き,溶岩流は停止しているように見え,海蝕崖や砂州の発達が認められた(写真1).旧島は西側の一部に残されており,カツオ鳥とみられる海鳥が飛来している様子が観察された.


ストロンボリ式噴火:
スコリア丘の山頂火口(直径50-60 m)から数10秒〜1分程度の間隔で濃い茶褐色の噴煙を勢い良く上げている.噴煙には弾道放出物が伴われることが多い.弾道放出物は,大きいものは長径数 m,固化したマグマだけでなく流動性のある状態,すなわちスパッター(溶岩のしぶき状の塊)として噴出しているものもあることが映像や画像から判読できる(写真2).噴煙の継続時間は数十秒程度で,まず淡褐色の弱い噴煙が生じ,その直後に勢いのある濃い茶褐色噴煙が上昇,そして徐々に弱まりながら薄い褐色へと変わり沈静化するという推移が一般的である.上昇速度が早い勢いのある噴煙は概ね1分以内の継続時間で,比較的長い静穏の後に起こることが多い.そのような,間欠的で勢いのある噴煙には多数の弾道放出物が伴われる.弾道放出物は,小さいものは火口上100 m程度まで上昇し,スコリア丘中腹まで到達する場合があるが,大きいものを含め多くは火口近傍に着弾するか,火口内に戻っている.夜間には噴煙の根本が赤熱し,灯台のような様相を呈している.赤熱した比較的大きな弾道放出物が飛散する様子は,肉眼でも観察することができた.
調査中,噴煙は常時南西からの風の影響を受け,ほとんどの場合上昇しつつ北東方向へ流れていた.噴煙高度は数100〜500 mで,風の強度により高度が異なっているようであった.噴出直後には濃い褐色噴煙であるが,島から離れるにつれて火山灰が噴煙から沈降・離脱し,噴煙の色は徐々に薄れて白色となる.噴煙軸付近では,西之島から4.5 km以上離れた場所ではほぼ白色の噴煙となっているが,黒色火山灰の降灰や火山ガス臭が認められた.
写真2(左上)ストロンボリ式噴火を繰り返し,勢い良く噴煙を上げるスコリア丘.手前は海に流れ込み水蒸気の白煙を上げる溶岩流.スコリア丘の東麓(右手)に溶岩流の給源と考えられる小火口丘が認められる.南側から撮影(6月15日12:26).(右上)噴火に伴う濃褐色噴煙と弾道放出物.噴煙は西からの風の影響を強く受けている(6月17日6:19).(左下)弾道放出物の拡大(6月15日14:14).最大長径は数m程度.不規則な形状を示し,溶岩のしぶき状の塊(スパッター)として噴出しているものもある(右下)南西から撮影した夕暮れ時の噴煙.噴煙の根本が赤熱している(6月16日18:58)
溶岩流:
西之島の南東端では溶岩流が海に流入し,水蒸気の白煙を上げている(写真3).スコリア丘東側には小火口丘(標高約 100 m)が形成されており,火口付近からは白煙が立ち上がっている.小火口丘の北側は火口壁の一部を構成し,明瞭な地形的高まりとして認められるが,小火口丘南側から南東海岸にかけては緩い斜面が続き,途中に白煙が上がっている箇所が複数ある.地形的特徴や白煙の分布状況,赤外カメラによる熱画像をもとにすると,溶岩流は小火口丘の麓,標高70-80 m付近から流出し,南東斜面を流下して島の南岸で海に流れ出ている.
南東端で海に流入する溶岩流は,水平距離にしておよそ 800 mに渡り分布しているが,水蒸気を上げている部分は局所的で10カ所以上ある.溶岩流は海岸付近では複数のローブ(舌状・袋状の構造)に分岐しており,それぞれの先端が海水と接触し水蒸気を上げている.水蒸気は時折激しく上がることがある.夜間は海に流入する溶岩ローブの先端が赤熱し,その分布が明瞭に認識できる(写真4).南東部の活動的な溶岩流では,先端部以外の場所も,高解像度写真では局所的に陽炎のように像が揺らいで観察され,赤外カメラでも高温を示した.一方それ以外の古い溶岩流も赤外カメラでは周囲大気よりもやや高い温度を示した.
写真3(左)島の南東端で海に流入する溶岩流(6月15日13:49).(右)スコリア丘東山腹に形成された小火口丘とその麓から南東に流れ出ている溶岩流(6月15日12:25)
写真4 赤外カメラで撮影した西之島.(左)南東から撮影(6月16日19:56).(右)南西から撮影(6月17日19:43).海に流出している溶岩流の先端部と火口から上昇する噴煙の様子が高温部として認められる.南東側ではスコリア丘東麓から続く内陸部の溶岩も,先端ほどではないが高温を示す.南西側からの画像では,古い溶岩も周囲大気よりやや高い温度を示す.
火山灰:
6月13~17日の間の複数回,噴煙下を航行するタイミングを見計らい船橋および船首甲板部に火山灰採取用トレイを設置し,火山灰を採取した.火山灰は,長径~数100 μm 以下で光沢のある透明度の高い褐色ガラス,黒色ガラス,結晶片,岩片により構成される.ガラス質火山灰は,平滑な破断面を有するもの,ガラスが引き延ばされたことによる鋭利な部分や滑らかな曲面を有するもの,Bubble wall型のもの,また,ごくまれに極度に引き延ばされて毛髪状の形態となっているものが存在する.これらはいずれも低粘性マグマによるストロンボリ式噴火に典型的に認められる火山灰の特徴であり,現在活動中のマグマに由来する本質ガラスと考えられる.また,多くの弾道放出物が火口内に戻っている様子(Fall back)が観察されていることから,火口内でリサイクルされたガラス片,岩片も同時に噴出していると考えられる.
図 1 (左上) 火山灰の全体像. (右上) 火山灰粒子の拡大.透明度のある褐色~黒色粒子で発泡度は多様である. (左下) いくつかの特徴的な形態を有する火山灰粒子.小目盛100 μm,大目盛 1 mm.(右下) 褐色ガラス質粒子の拡大.顕著なガラス質光沢を有する.
(火山噴火予知研究センター:前野深)
西之島における噴火活動について(続報)
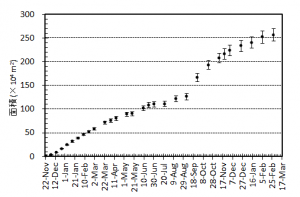
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2015年2月27日 (JST) までの状況についてまとめた.島の大きさは東西2 km 南北1.8 km,面積はおよそ 2.6 km2 である.溶岩流の北側への延伸は止まったものの,2月以降拡大が再開した東側ではゆっくりと島の成長は続いており,依然として溶岩が供給されている.中央火砕丘の成長も継続しており,火口直径は90 m ほどになっている.噴出量はおよそ1億 m3,噴出率は15-20万 m3/day と推定される.島の成長は鈍化しているが,これは溶岩が徐々に深くなる斜面を埋め立てているためであり,溶岩流出率は大きくは変化していない.噴火活動は依然として活発と推定される.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
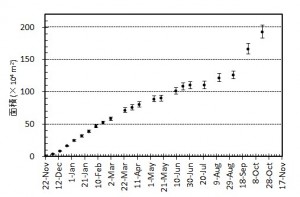
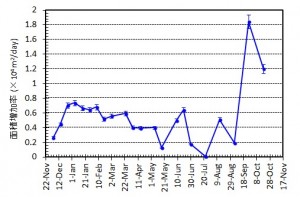
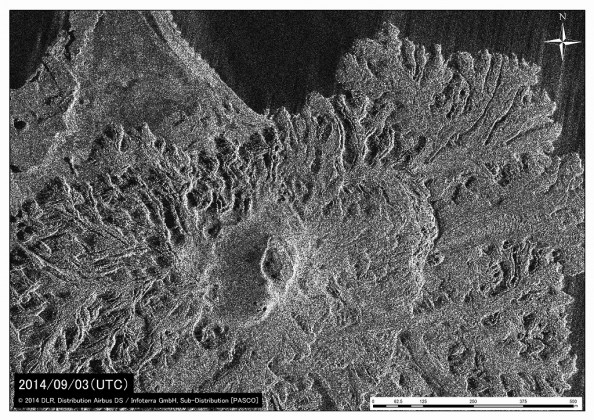
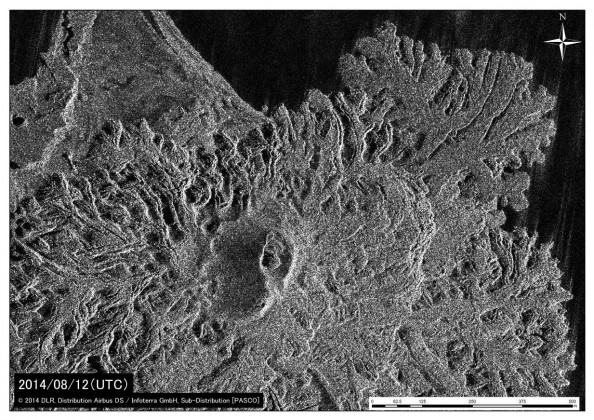
[面積変化]図2 東側溶岩ローブ群および中央火口の様子.上図が2月5日(JST),下図が2月27 日(JST).中央火砕丘の火口径は直径 90 m 程度,火口縁の輪郭がはっきりとしてきた. TerraSAR-Xによる衛星画像 (協力: 株式会社パスコ).
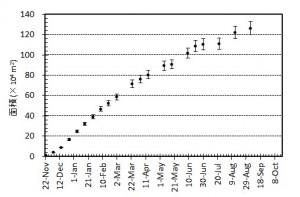
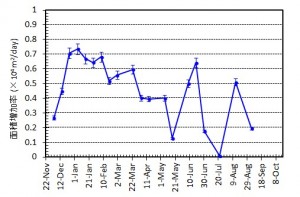
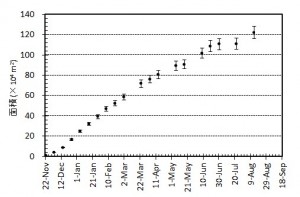
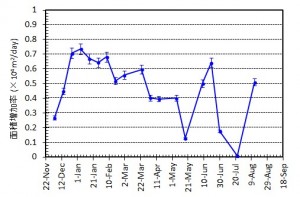
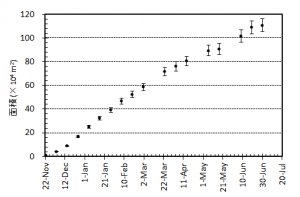
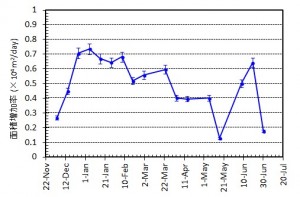
図3 西之島の新たに形成された部分の面積変化(左)および面積増加率(右).エラーバーは海岸線の読み取り精度から生じる誤差.
[噴出量および噴出率]
[参考資料・ホームページ]
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報: http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- 株式会社パスコ 西之島噴火活動モニタリング: http://www.pasco.co.jp/disaster_info/141118/
(火山噴火予知研究センター:中田節也)
西之島の火山活動(2014年3月4日)
- 観測日:午後2時〜2時半。午後6時10分〜6時45分。
- 途中硫黄島で給油。
- 使用航空機:朝日新聞社機「あすか」Citation Encore
- 天候:晴れ。南西の風。
噴火開始から1年3ヶ月を過ぎた西之島では,活発な噴火活動が続いている。これまで溶岩が中央やや南に位置する火砕丘の麓から方向を変えて流れ続け,島の面積はしだいに拡大してきた。観察中は,その火砕丘からストロンボリ式噴火が連続的に発生し,爆発で吹き飛んだ溶岩片(火山弾およびスコリア)が火口の周囲に堆積し続けていた。火山灰噴煙は火口の上約百m上昇し,白色となって,そのまま数km北東に流れている。一方,溶岩は溶岩チューブシステムを使って東側に流れそのまま海に流入し,海岸線数百mにわたって白色の水蒸気が上昇している(写真1,2)。そこでは,新しい溶岩が海岸の手前数百mのところで,すでに固まった溶岩の表面を複数箇所で突き破り,そのまま地表を流れて海に突っ込んでいる。新しい溶岩流は両側に堤防が発達し、中央をより暗色で表面ががさがさの溶岩が占めている。夜間は新しい溶岩部分だけが赤熱している(写真3,4)。
中央の火砕丘では,ストロンボリ式噴火が継続しており,数秒から数十秒間隔で爆発が繰り返して起こり,数秒間隔で爆発が連続する(写真5)。火砕丘の頂部はすり鉢状に凹んだ火口であり,火口の表面はスコリアや火山弾が覆っており,溶岩は直接火口底まで出現していない。
※ 報道関係の方へ:写真の引用については,朝日新聞社にお問合せください





(火山噴火予知研究センター:前野深)
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年2月5日 (JST) までの状況についてまとめた.島の大きさは東西2 km 南北1.8 km,面積はおよそ 2.5 km2 である.昨年9月以降続いていた溶岩流の北側への延伸は止まったものの,溶岩供給は継続しており,東側に新たな溶岩ローブを形成し,拡大を続けている.新たな溶岩は傾斜20度程度の斜面にせり出し始めており,その先端は最も深い部分で水深100 m近くに達していると考えられる.一方中央火砕丘も成長し続けており,すり鉢状の大火口内の中央にはさらに凹部が認められ,拡大を続けている.噴出量は9500 万±1000 m3,噴出率は一時低下したものの再び増加し,およそ30万 m3/day と推定される.島の成長は一時鈍化したものの,溶岩流出と中央火砕丘の成長は衰えておらず,活発な活動は依然として続いている推定される.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]
[噴出量および噴出率]
[参考資料・ホームページ]
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報: http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- 株式会社パスコ 西之島噴火活動モニタリング: http://www.pasco.co.jp/disaster_info/141118/
(火山噴火予知研究センター:前野深)
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年12月23日 (JST) までの状況についてまとめた.島の大きさは東西1.7 km 南北1.8 km,面積はおよそ 2.3 km2 である.溶岩流の北西側への延伸,溶岩膨張割れ目の発達は継続しており,溶岩は北側全域に供給されていると考えられる.また西側へ流出した溶岩により,残されていた旧島は埋没寸前になっている. 噴出量は8000~9000 万 m3,噴出率はやや減少し,10-20万 m3/day と推定される.島の成長は鈍化しているものの,中央火砕丘の大火口は再び拡大して 80 m 程度になっており,活発な活動は継続していると推定される.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]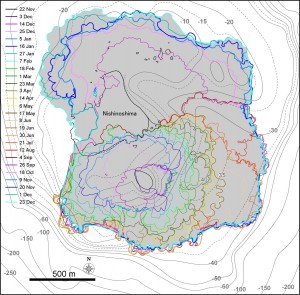
図2 9月以降成長を継続している北側溶岩ローブ群.左図が12月1日(JST),右図が12月23 日(JST).TerraSAR-Xによる衛星画像 (協力: 株式会社パスコ).中央火砕丘の火口径は12月23日時点で直径 80 m 程度である.旧島は溶岩流により埋没寸前である.
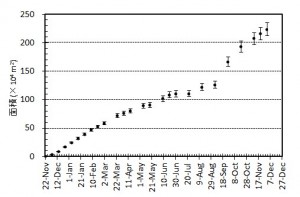
図3 西之島の新たに形成された部分の面積変化(左)および面積増加率(右).エラーバーは海岸線の読み取り精度から生じる誤差.
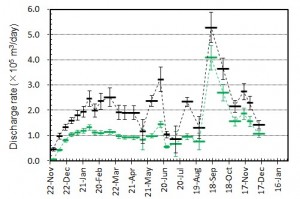
[噴出量および噴出率]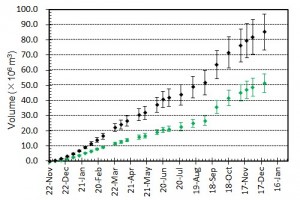
[参考資料・ホームページ]
海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
国土地理院における西之島付近の噴火活動関連情報: http://www.gsi.go.jp/gyoumu/gyoumu41000.html
株式会社パスコ 西之島噴火活動モニタリング: http://www.pasco.co.jp/disaster_info/141118/
(火山噴火予知研究センター:前野深)
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年12月1日 (JST) までの状況についてまとめた.島の大きさは東西1.7 km 南北1.8 km,面積はおよそ 2.2 km2 である.溶岩流の北~北西側への延伸,溶岩膨張割れ目の発達の様子から,溶岩は継続的に北側全域に供給され,浅海を埋め立てながらゆっくり前進し続けていると考えられる.一方,中央火砕丘の大火口は,埋積が進み直径が10月より小さく 60 m 程度になっているが,標高はやや高くなり,成長は継続していると推定される.噴出量は 8500±1000万m3,噴出率は10月よりやや低下したものの,25-30万 m3/day の水準は維持しており,活動は依然として活発である.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]
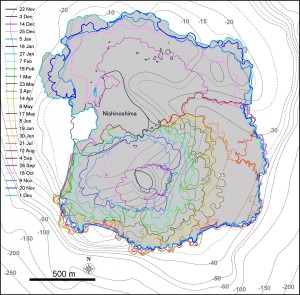

図3 西之島の新たに形成された部分の面積変化(上)および面積増加率(下).エラーバーは海岸線の読み取り精度から生じる誤差.
[噴出量および噴出率]
[参考資料・ホームページ]
海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
国土地理院における西之島付近の噴火活動関連情報: http://www.gsi.go.jp/gyoumu/gyoumu41000.html
株式会社パスコ西之島噴火活動モニタリング: http://www.pasco.co.jp/disaster_info/141118/
(火山噴火予知研究センター:市原美恵・西田究)
西之島火山の活動 –父島での空振モニタリングで判明-
父島の気象観測所に設置したオンライン空振観測点のデータと,気象庁地震観測点の東西成分を用いて,西之島火山の空振モニタリングを開始しました.
観測点の位置を,図1に示してあります.三日月山観測点の地震計東西成分(JMA.CHJI3.EW)と気象観測所の気圧計(EV.CHI.NB)の相関を取ることで,西之島火山の活動をモニターする事が出来ます.
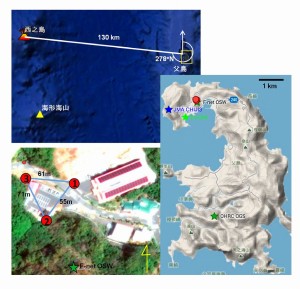
図2の上段のグラフは,地震計と気圧計の振幅を表しています.青が三日月山の地震計東西成分,緑が気象観測所の気圧計の振幅です.また,下段の図で,縦軸ゼロ付近の赤と青のパターンが,西之島火山の空振を検出していることを意味しています.そして,中段のグラフが,マイクの信号の中にどのくらい空振が入っているかを示すものです.割合が小さくなる原因として,(1)風のノイズが大きくなる,(2)空振が小さくなるの2つが考えられます.(1)の場合には,振幅が大きくなって中段のグラフが小さくなるはずですが,多くの場 合そうなっていませんので,(2)が原因だと考えられます.つまり,空振の到来の有無がちゃんと計測されているようです.
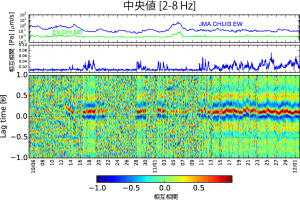
10月28日以降,間欠的な空振活動が何回か見られましたが,11月13日からほぼ連続的に検出されています.間欠的な活動が何回か起こったあと、連続的に噴火に移行したようです.このように長く空振が続くのは,空振観測を始めて以来2回目で,前回は5月半ばから6月半ばに見られました.
謝辞:空振観測に当たっては,小笠原村役場,気象庁のご協力を得ています。記して感謝します。
(火山噴火予知研究センター:前野 深)
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年11月9日 (JST) までの状況についてまとめた.島の大きさは東西1.6 km 南北1.8 km,面積はおよそ 2 km2 である.9月以降の北側への拡大は継続しており,旧西之島は北西の高まり(標高約20 m)を除き新たな溶岩流に覆われている.溶岩流の延伸と溶岩膨張割れ目の発達の様子から,北側全域に溶岩が供給され続けていると考えられる.中央火砕丘の成長も継続し,火口径は10月より拡大して直径 70 m 程度と推定される.噴出量は 8000±1000万m3,噴出率は10月よりやや低下したものの,20万 m3/day を超える水準で,活動は依然として活発である.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]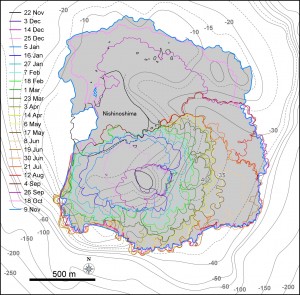


11月9 日(JST).TerraSAR-Xによる衛星画像 (協力: 株式会社パスコ).中央火砕丘の火口径が直径 70 m 程度まで拡大している.
図3 西之島の新たに形成された部分の面積変化(上)および面積増加率(下).エラーバーは海岸線の読み取り精度から生じる誤差.
[噴出量および噴出率]
[参考資料・ホームページ]
海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
国土地理院における西之島付近の噴火活動関連情報: http://www.gsi.go.jp/gyoumu/gyoumu41000.html
株式会社パスコ西之島噴火活動モニタリング: http://www.pasco.co.jp/disaster_info/131122/
(火山噴火予知研究センター:中田節也)
西之島の噴火活動:北側への溶岩流出と南よりの火砕丘でストロンボリ式噴火を継続。 西之島旧島(黄色っぽい低地)は溶岩平原の西端にわずかに残っている。溶岩が海に注入している場所からは水蒸気が上がっている。2014年11月13日昼頃,朝日新聞社機から上空と海上から中田が撮映。
※報道関係の方へ:朝日新聞社の協力により撮影しています。画像の引用については、朝日新聞社にお問合せください。
*画像をクリックすると動画が再生されます
(火山噴火予知研究センター:前野 深)
西之島における噴火活動について(続報)
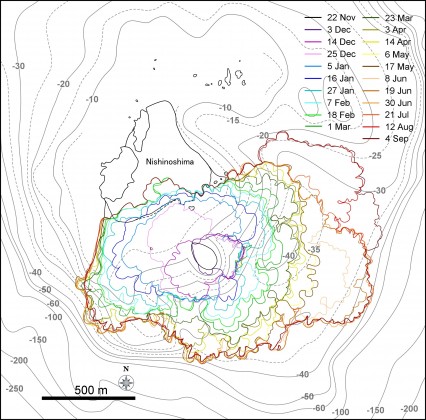
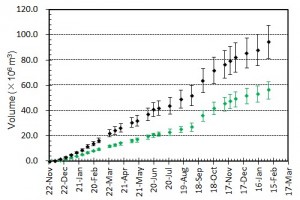
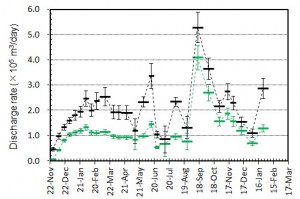
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年10月18日 (JST) までの状況についてまとめた.島の大きさは東西1.6 km 南北1.7 km,面積はおよそ 1.9 km2 である.9月以降北側へ大きく拡大し,旧西之島は北西の高まりを残してほぼ新たな溶岩流に覆われた.溶岩流は中央火口丘の北側を崩して溶岩ローブ群を形成した後,さらにその先端を破り複数個所から樹枝状に分岐して現在の形状に成長したと考えられる.8月に主火口内に確認された溶岩ドーム状の高まりや火口凹地形は,火砕丘の成長により消滅した.北側への拡大は継続し,海底火山体山頂北端に迫っている.噴出量は 7000±1000万m3,噴出率は9月26日までの期間より下がったものの,30万 m3/dayの高い水準であり,活動は依然として活発である.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]図1(左)西之島の新たに形成された部分の輪郭の変化.(右)期間毎のおよその溶岩流の分布.TerraSAR-Xによる衛星画像 (協力: 株式会社パスコ) をもとに作成している.海底地形は海上保安庁水路部 (1993) の海底地形図をもとにしている.
図2 9月以降に新たに形成された北側溶岩ローブ群.左図が9月26日(JST),右が10月18日(JST).TerraSAR-Xによる衛星画像 (協力: 株式会社パスコ).9月には北側への溶岩流出により火砕丘が崩れている様子が認められたが,10月に入り火砕丘は崩壊地形を埋めて再び成長した.8月に認められた主火口内の溶岩ドームとみられる地形的高まりや火口凹地形は消滅した.
図3 西之島の新たに形成された部分の面積変化および面積増加率.エラーバーは海岸線の読み取り精度から生じる誤差.
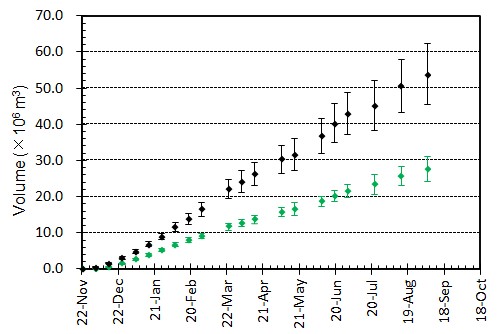
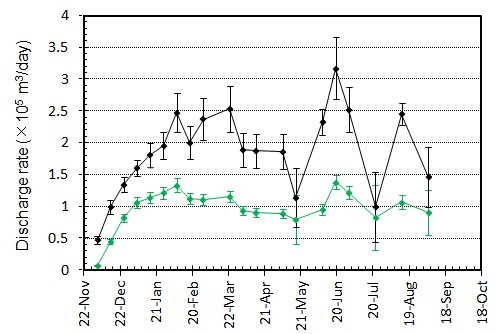
[噴出量および噴出率]図4 噴出量とその変化.黒はトータルの噴出量.緑色は陸上部分の体積.エラーバーは,海岸線の読み取り誤差,海水面上の溶岩の比高と水深の不確かさから生じる誤差.陸上部分の体積については,国土地理院による測量データ(2,3,7月)とその後の経過等をもとに推定されるおよその平均溶岩厚さと山頂標高の増加曲線をもとに見積もっている.
図5 噴出率(1日当たりの噴出量)とその変化.黒はトータルの噴出率.緑色は陸上のみに対する噴出率.図4の噴出量ダイアグラムをもとに見積もっている.エラーバーは,海岸線の読み取り誤差,海水面上の溶岩の比高と水深の不確かさから生じる誤差.
[参考資料・ホームページ]- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報: http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- 株式会社パスコ 西之島噴火活動モニタリング: http://www.pasco.co.jp/disaster_info/131122/
(火山噴火予知研究センター:前野 深)
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年9月4日 (JST) までの状況についてまとめた.島の大きさは東西1.6 km 南北1.2 km,面積はおよそ 1.25 km2 である.東側への溶岩流出は継続しており,埋め残されていた東側の浅海部分はほぼ埋め尽くされた.島の東端はやや延伸し,海底山体の斜面に達している.一方,8月13日に撮影されたTerraSAR-X衛星画像 (協力: 株式会社パスコ) で主火口内に確認された溶岩ドーム状の高まりや火口凹地形は不明瞭になっており,主火口内が溶岩でほぼ満たされたと推定される.噴出量はおよそ5000-6000万m3,噴出率は変動しているものの10万 m3/day を超える水準を維持しており,活動は依然として活発である.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]
図3 西之島の新たに形成された部分の面積変化および面積増加率.エラーバーは海岸線の読み取り精度から生じる誤差.面積増加率は減少を続けた後,5月以降大きく変動している.
[噴出量および噴出率]
[参考資料・ホームページ]
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報 http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- 株式会社パスコ 西之島噴火活動モニタリングhttp://www.pasco.co.jp/disaster_info/131122/
(火山噴火予知研究センター:前野 深)
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年8月13日までの状況についてまとめた.島の大きさは東西1.55 km 南北1.2 km,面積はおよそ 1.2 km2 である.6月以降継続していた東側への拡大は7月下旬までに停止したものの溶岩供給は継続し,7月下旬からは北東部で溶岩が流出し始め,一旦減少した面積拡大率が再び増加に転じている.東西および南方向では,海蝕による島の縮退が若干認められる.一方,8月13日(UTCでは12日)に撮影されたTerraSAR-X衛星画像 (協力: 株式会社パスコ) によると,北側の火口群が合体して大火口を形成するとともに,火口内に直径50 mほどの溶岩ドームとみられる高まりが形成されていることがわかった.噴出量はおよそ5000万m3,噴出率は5月中旬以降変動しているものの10万 m3/day を超える水準を維持しており,活動は依然として活発である.また,溶岩ドーム形成は火口の閉塞を意味するため,今後ブルカノ式噴火等の爆発的な噴火を起こす可能性がある.噴出率,火口形状,溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]
図3 西之島の新たに形成された部分の面積変化および面積増加率.エラーバーは海岸線の読み取り精度から生じる誤差.面積増加率は減少を続けた後,5月以降大きく変動している.
[噴出量および噴出率][参考資料・ホームページ]
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」,p. 47.
- 国土地理院における西之島付近の噴火活動関連情報 http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- 株式会社パスコ 西之島噴火活動モニタリングhttp://www.pasco.co.jp/disaster_info/131122/
(火山噴火予知研究センター:市原美恵)
父島で捉えた西之島火山の活動に伴う空振
小笠原諸島・西之島では,活発な噴火活動が続いているが,観測情報は非常に限られている.そこで,一般にアクセス可能な最近接の陸地である小笠原村父島に空振計を設置し,西之島の噴火活動に伴う空振の観測を試みた.父島は,西之島東方130km の距離にある.遠距離での空振観測は,大気構造の影響で伝播経路が曲げられ,まったく届かなくなることも多いが,大気構造によってはシグナルを捉えられる可能性もある.2014年4月25日から連続観測を開始し,6月9日までのデータを解析した.その結果,西之島火山方向からの空振が,5月12日の夜以降頻繁に届くようになったことが分かった.振幅の大きなシグナルは,父島と母島の地震計でも捉えられており,その到来時刻の差から,西之島からの空振であることはほぼ間違いない.海上保安庁による航空機観測では,4月15日と5月21日の間に新しい火口が開いたことが報告されており,また,衛星観測(TerraSAR-X, パスコ)は,5月6日と17日の間に,西之島東側への溶岩流出が始まったことを示している.父島における空振観測によって,西之島火山の活動状況を高い時間分解能で把握できる可能性がある.
謝辞:
空振観測に当たっては,小笠原村役場,JAMSTEC,川上和人氏(森林総合研究所),鴨川仁研究室(学芸大学)のご協力を得ている.
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年6月30日までの状況についてまとめた.島の大きさは東西1.6 km 南北1.1 km,面積はおよそ 110万m2 である.東側への溶岩流出が継続して島が拡大しているほか,主火口群の北側と南側へも新たな溶岩が流出し,これまでの溶岩を覆い始めている.面積増加率は6月に入り増加に転じたものの,その後再び減少している.ただしこれは東側に流出した溶岩が海底火山体の山頂火口縁を超えて深い方向に拡がっているためで,噴出率(およそ25-30万 m3/day)は大きく変わっていないと推定される.噴出量は4000-5000万m3 で,1973-74年噴火の噴出量のおよそ2倍に達している.溶岩の供給は継続しており,活動は依然として活発な状態にあるといえる.噴出率の推移や溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]
図3 西之島の新たに形成された部分の面積変化および面積増加率.エラーバーは海岸線の読み取り精度から生じる誤差.面積増加率は減少を続けた後,6月に入り増加に転じたもののその後再び減少している.ただしこれは東側に流出した溶岩が海底火山体の山頂火口縁を超えて深い方向に拡がっているためで,下記のように噴出率は大きく変わっていない.
[噴出量および噴出率]
[参考資料・ホームページ]- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報
- http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- 株式会社パスコ 西之島噴火活動モニタリング
- http://www.pasco.co.jp/disaster_info/131122/
西之島における噴火活動について(続報)
概要: 西之島の噴火活動で新たに形成された部分の面積,噴出量,噴出率について2014年5月6日までの状況についてまとめた.島の大きさは東西1400 m 南北1100 m,面積はおよそ 90万m2 である.面積増加率は減少傾向にあり,見かけ上の成長は鈍化しているが,これは溶岩流が水深の深い方向へ拡大しているためである.これまでの噴出量は2800万~3500万m3 で,1973-74年噴火の噴出量(およそ2400万m3)を上回ったと推定される.噴出率は2~3月のピーク時よりやや減少し,4~5月では20万 m3/day程度と推定される.また,衛星画像をもとに溶岩表面構造の時間変化を調べたところ,大部分で溶岩ローブ群の膨張を示す亀裂の形成・拡大が進行していることがわかった.これらのことから,溶岩の供給は継続しており,活動は依然として活発な状態にあるといえる.噴出率の推移や溶岩表面構造の時間変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化][噴出量および噴出率]
溶岩表面における開口亀裂の発達の様子(図5,6)と,亀裂形成域で標高が増加していること(2014年2月16日と3月22日の国土地理院の地形データにもとづく)から,開口亀裂はlava inflation cleftと解釈できる.すなわち,溶岩ローブ群に継続的に溶岩が供給されて内圧が高まることにより溶岩ローブが膨張し,表面の皮殻が壊れて亀裂が生じていると解釈できる.開口亀裂の形成と発達は5月上旬の時点でまだ継続しており,溶岩流出は衰えていないと判断できる.溶岩表面構造の時間変化は今後の活動推移を予測する上でも重要と考えられる.
※ モニタリング及び衛星画像提供:株式会社パスコ
(火山噴火予知研究センター:前野 深)
[参考資料・ホームページ]
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報 http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- 株式会社パスコ 西之島噴火活動モニタリングhttp://www.pasco.co.jp/disaster_info/131122/
西之島における噴火活動について(続報)
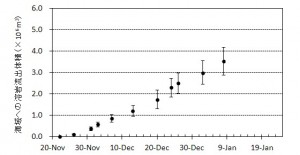
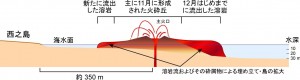
概要: 西之島の噴火活動は依然として活発な状態にある.新たに形成された部分の面積,海域への溶岩流出体積,流出率の変化について1月8日までの状況についてまとめた.島の大きさは東西650 m 南北550 m,面積は,1973-74年噴火時に新島が最も成長した時(新島出現からおよそ1年後)の大きさ約26万m2に達している.海域への溶岩流出体積は300万m3超,流出率は多少の上下変動を伴うものの依然として105 m3/dayもしくはそれをやや下回る程度を維持していると推定される.噴出率の変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]
[溶岩流出体積および流出率]
※ 溶岩流出以前(11月21日)の新島の楕円状の海岸線を基準に,溶岩流の分布と噴火前の地形をもとに仮定した水深(溶岩流出前の水深)を用いた差分から,およその溶岩体積を推定している.毎回30 %程度の誤差が含まれる.
※期間毎の面積(溶岩流分布)の変化量(推定最大値および最小値を用いた差分),および噴火前の地形をもとに仮定した水深(溶岩流出前の水深)を用いた差分から,溶岩流出率を推定している.
[参考資料]- 海上保安庁海洋情報部海域火山データベースhttp://www1.kaiho.mlit.go.jp/GIJUTSUKOKUSAI/kaiikiDB/kaiyo18-2.htm
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報http://www.gsi.go.jp/gazochosa/gazochosa60010.html
- http://www.gsi.go.jp/gyoumu/gyoumu41000.html
- JAXA衛星利用推進サイト: http://www.sapc.jaxa.jp/topics/2014/news0110.html
(火山噴火予知研究センター:前野 深)
西之島における噴火活動について
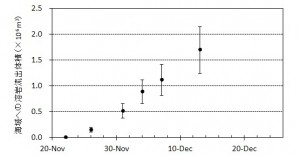
概要: 西之島沖の噴火により成長していた新島は,2013年12月25日頃に西之島と接合し,一体化した.新たに形成された部分の面積,海域への溶岩流出体積,流出率の変化について12月26日までの状況についてまとめた.面積はおよそ16万m2,海域への溶岩流出体積は200万m3超,流出率は依然として105 m3/day程度を維持していると推定される.この噴出状況が維持されている場合,2014年1月に入った時点で,新たに形成された部分は旧西之島の面積を上回っている可能性が高い.噴出率の変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
[面積変化]
[溶岩流出体積および流出率]
*溶岩流出以前(11月21日)の新島の楕円状の海岸線を基準に,溶岩流の分布と噴火前の地形をもとに仮定した水深(溶岩流出前の水深)を用いた差分から,およその溶岩体積と流出率(期間中の一日当たりの流出量)を推定している(12月8日資料を参照).なお,国土地理院が公開した12月3日,17日の新島の立体図を参考にして,溶岩流厚さの見積もり最大値をこれまでの報告より下方修正した.それに伴い溶岩体積と流出率についてもエラーバーの上限値が変わり,12月20日以前は当初の見積もりよりやや低くなっている.
[参考資料]- 海上保安庁海洋情報部海域火山データベースhttp://www1.kaiho.mlit.go.jp/GIJUTSUKOKUSAI/kaiikiDB/kaiyo18-2.htm
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報
- http://www.gsi.go.jp/gazochosa/gazochosa60010.html
- http://www.gsi.go.jp/gyoumu/gyoumu41000.html
観察日時:2013年12月26日 12:30-13:00
撮影者:中田節也
毎日新聞社機:Cessna Citation CJ2+
説明:11月20日に発見された火山新島では,海水とマグマが接触する激しい爆発(マグマ水蒸気爆発)を経て,11月24日から溶岩が流出し続けている。この間,新島は大きく成長し,12月26日に西之島と合体した。
※ 報道関係の方へ: 毎日新聞社の協力により撮影しています.動画の引用については,毎日新聞社にお問合せください.
(火山噴火予知研究センター:中田節也)
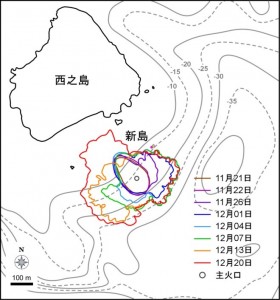
朝日新聞社の取材機(ジェット/あすか)に同乗し, 2013年12月25日に西之島の観察を行った.この結果,2013年11月に形成された新島(以下2013年新島と仮称)の北西への成長が進み,旧来の西之島新島と接合していることが確認された.
観測日時:2013年12月25日15時13分~43分(観察者/金子)
地形:2013年新島は北西―南東方向にやや伸長した“三つ葉型”をしており,南東側が高く,北西に向かってなだらかな溶岩流の堆積面が伸びている(写真1).長径は約600m,短径は約300m,高さは約50m程度と見られる.
火口と噴出物:火口は島の南東域に3か所が認められる(写真1).1つは高さ約50mの火砕丘頂部にある主火口(写真1 a)で,ここでは1~2分に1回程度の頻度でストロンボリ式噴火が発生し,赤熱したマグマ片が周囲に飛ばされている(写真2 f).2つ目はその北側斜面低位に位置する火口(写真1 b)で,ここからは火山灰を多く含む噴煙が盛んに立ち昇っている.3つ目が主火口の西,島の中央部に近い場所にある火口(同c)で,ここから北西に向かって溶岩流が噴出し,途中から銀杏の葉状に複数のローブに分かれ北西域一帯を覆っている(同d).ここでの爆発的噴火は見られない.この噴出により島が一挙に成長し西之島新島と接合することとなった. 最新のローブは東側に向かい,海岸線付近で盛んに水蒸気を挙げている(写真2 g) .
西之島新島と2013年新島との接合部:両島は間に細長い湖(100数十m × 数十m) (写真1 e)を挟んで東側(写真3)と西側(写真4)で接合している.接合部の長さは共に10m 程度である.高い波が押し寄せた際は,接合部を乗り越え,海水が湖側に流入している.湖は2013年新島の成長により海水が両島の間にトラップされたものと考えられ,溶け込んだガス成分によって赤褐色を呈している.
※ 報道関係の方へ: 朝日新聞社の協力により撮影しています.写真の引用については,朝日新聞社にお問合せください.
(火山噴火予知研究センター:金子隆之)
西之島沖での新島成長過程(続報)
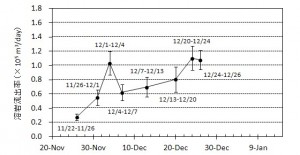
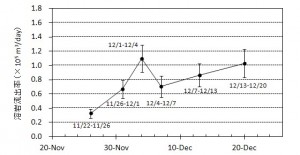
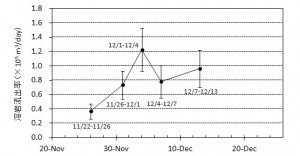
概要: 西之島沖で噴火を継続している新島の面積,海域への溶岩流出体積,流出率の変化について12月20日までの状況についてまとめた.20日現在,面積は12万m2弱,海域への溶岩流出体積はおよそ200万m3,流出率はやや増加傾向にあるものの依然として105 m3/day程度を維持していると推定される.噴出率の変化は今後の活動推移を予測する上で重要であり,引き続き注視していく必要がある.
新島の面積変化
※溶岩流出以前(11月21日)の楕円状の海岸線を基準に,溶岩流の分布と噴火前の地形をもとに仮定した水深(溶岩流出前の水深)を用いた差分から,およその溶岩体積と流出率(期間中の一日当たりの流出量)を推定している(12月13日報告および図4を参照).なお,国土地理院が公開した12月3日の新島の立体図を参考にして,溶岩流厚さの見積もり最大値をこれまでの報告より下方修正した.それに伴い溶岩体積と流出率についてもエラーバーの上限値が変わり,12月7日以前は当初の見積もりよりやや低くなっている.
※ 海底地形図が作成された90年代から時間が経過しており,当時よりも水深10 m前後の浅海部が沖側へ拡大している可能性がある(西之島本島の浸食が進んでおり,南東側に物質が供給されている可能性など).また,11月20日以前の浅海底での活動に伴う堆積作用も考えられるため,やや浅い水深の場合も仮定している.
参考資料
- 海上保安庁海洋情報部海域火山データベースhttp://www1.kaiho.mlit.go.jp/GIJUTSUKOKUSAI/kaiikiDB/kaiyo18-2.htm
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報 http://www.gsi.go.jp/gazochosa/gazochosa60010.htmlhttp://www.gsi.go.jp/gyoumu/gyoumu41000.html
観察日時: 2013年12月20日 12:20-13:05
観察者: 前野 深
使用機体: 毎日新聞社ジェット機(希望)
概要
西之島南東沖の新島の噴火活動は依然として活発であり,ストロンボリ式噴火と溶岩流出が継続している.新島は12月初旬と比べて南西から北西側にかけて大きく成長しており,大きさは南北約450 m 東西約450 mに達している(写真 1, 2).主火口の位置に大きな変化はないものの火砕丘が再び成長したことにより,新島の海水面からの高さは西之島の2倍近い40~50 mに達していると推定される.
主火口付近の活動
主火口では数十秒~数分の周期でストロンボリ式噴火が繰り返し発生し,火砕丘が成長している(写真 3, 4).火砕丘は,溶岩流出により一部崩壊したすり鉢状火口や東側溶岩の上に新たに成長し,裾野を広げている.また,火砕丘の東側斜面には小火口が少なくとも2箇所あり,主火口のストロンボリ式噴火とは別に勢いのある褐色噴煙が上がることがある(写真 5).
溶岩流
溶岩流出は火砕丘西側で継続している(写真1, 6).溶岩は大きく北西,南西,南東の3方向へ分岐して流動しているが,このうち南西へ向かう溶岩流はやや低い位置から流出している.溶岩と海水との接触により発生している水蒸気はとくに南西側溶岩で激しいが,北西および南東側でも発生しており,島のほぼ西側全域で溶岩が流動し面積を増加させていると考えられる.西之島との最短距離は70 m程度であるが,この部分の水蒸気量は少ない.水蒸気量が多く,活発に流動していると考えられる部分と西之島との距離はおよそ100 m程度である.また,新島東側の溶岩流は見かけ上停止しており,部分的に波による浸食が認められる.
※ 報道関係の方へ: 毎日新聞社の協力により撮影しています.写真の引用については,毎日新聞社にお問合せください.
西之島沖での新島成長過程(続報)
西之島沖で噴火を継続している新島の海域への溶岩流出体積,流出率の変化について12月13日までの状況についてまとめた(図1,2).
基本的には海上保安庁公表の空撮画像にもとづき※,溶岩流出(11月21日)以前の楕円状の海岸線を基準に,溶岩流の分布と噴火前の地形をもとに仮定した水深(溶岩流出前の水深)を用いた差分から,およその溶岩体積と流出率(期間中の一日当たりの流出量)を推定している(前回の報告および図3を参照).
※ 12月7日までは,国土地理院による空撮写真,およびその他メディア等により報道されている空撮写真等も参考にしている.
(火山噴火予知研究センター:前野 深)
概要
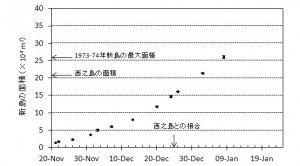
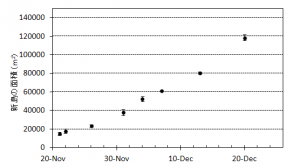
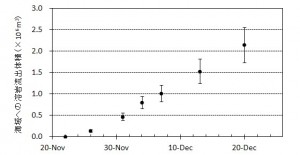
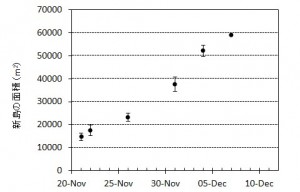
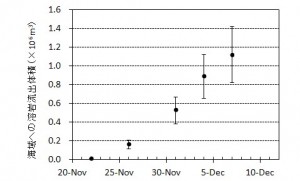
西之島沖で噴火を継続している新島の面積,海域への溶岩流出体積,流出率の変化について,海上保安庁,国土地理院などの空撮画像をもとに推定した.新島の面積は,12月4日におよそ5万m2に達しているが,島の成長速度は前回1973-74年噴火のおよそ8倍と非常に速いことがわかった.また溶岩流出率については,時間とともに増加し,11月末以降105 m3/dayに迫る付近で推移していると考えられる.この流出率は,前回形成された西之島新島を除き,国内で最も新しい火山島である昭和硫黄島形成時の平均溶岩流出率 ~1×105 m3/day(1935年1〜3月)に匹敵する.新島の面積変化や溶岩流出率の時間変化は今後の噴火活動推移を予測する上で重要であると考えられる.
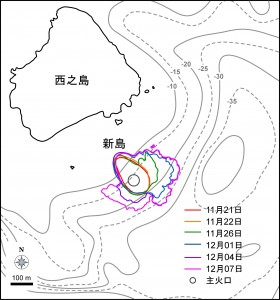
西之島沖での新島形成の経過
2013年
11月20日 北西−南東方向に伸びた楕円形の新島および変色域が海上保安庁により確認された.噴火開始地点は1973年噴火時の火口群の位置とほぼ同じである.
11月21日 コックステールジェットを伴うマグマ水蒸気爆発(典型的なスルツェイ式噴火)が断続的に発生.新島の中央部には火砕丘が形成されている.
11月22日 新たな火口が東側に形成され,わずかに溶岩が流出し始めている様子が確認される(海上保安庁の空撮画像にもとづく).
11月24日 山頂火口からは断続的にストロンボリ式噴火を繰り返すとともに,火砕丘東側は新たな火口の形成と溶岩流出に伴い部分的に崩壊,クリンカーの発達した溶岩流は東側の50 mほど沖合まで流出.
11月26日 東側の溶岩流が成長を続け,新島は拡大.
12月1日 溶岩はさらに東側に向けて複数のローブを形成しつつ拡大.
12月4日 南西側にも溶岩を流出してやや拡大.
12月7日 西側の溶岩流出が継続.
※ 11月20日以前の観測記録がないが,海水面上に到達するまでの浅海底での噴火のステージがあったと推定される.1973年噴火の際には,変色水が確認されてから今回の11月20日に観察されたような火砕丘状の新島になるまでに,およそ5ヶ月を要している(小坂, 1991など).
新島の面積変化
ホームページ上で公開されている海上保安庁,国土地理院による空撮写真,およびその他メディア等により報道されている空撮写真等をもとに新島の発達の様子を図1にまとめた.また,新島のおよその面積変化を図2に示す.海岸線の定義は難しいため誤差を含む.溶岩流出以降,島の面積は拡大し続け,2週間後の12月4日には5万 m2,12月7日にはおよそ6万 m2に達している.1973~74年噴火の際には,溶岩が流出して面積が5万 m2を超えるまでにおよそ2カ月要していることから(小坂, 1991),今回の噴火による新島の成長速度は前回の8倍と非常に速いことになる.
海底地形図(海上保安庁, 1993)をもとにすると,12月4日頃まで溶岩流の主要部分は,水深が徐々に深くなる東側へ向かい流動したと考えられる.溶岩流の進行方向,すなわち島の成長方向は海底地形の影響によるものと推定される.その後溶岩は南西側に方向を変えて流出し始めた.溶岩が南東側の埋め立ておよび冷却・固化により流動を妨げられ,新たな流路を選択するようになったことが一因として考えられる.
溶岩流出体積および流出率
噴火が開始したのは水深10~20 m付近,12月4日には溶岩流先端付近は噴火前の水深25~30 mに達したと推定される(図1).
溶岩流出以前の楕円状の海岸線を基準に,海に流出した溶岩流の面積および噴火前の地形をもとに仮定した水深を用いた差分から,およその溶岩体積(図3)と流出率(期間中の一日当たりの流出量,図4)を推定した.なお,増加した溶岩流の海水面上での比高は平均5 m (最小の場合) ~ 15 m(最大の場合)と仮定し,水深についても5 ~10 m程度の誤差を考慮している.
海に流入した溶岩の体積は徐々に増加し,1×106 m3 に迫っている.一方,溶岩流出率も徐々に増加し,12月1日~4日の4日間では平均1×105 m3/day程度であるが,その後やや減少している.
1934-35年昭和硫黄島噴火との比較
日本国内では西之島以外で最も新しい火山島である鹿児島県薩摩硫黄島沖の昭和硫黄島形成時には,溶岩流出期(1935年1〜3月の2ヶ月)の平均流出率は~1×105 m3/dayと推定されている(Maeno and Taniguchi, 2006).西之島の溶岩流出率は11月末以降,昭和硫黄島形成時の平均溶岩流出率に迫る付近で推移している.
※ 西之島と昭和硫黄島では岩石化学組成が異なるため(昭和硫黄島溶岩はデイサイト~流紋岩,西之島溶岩は安山岩と推定される),噴火メカニズムや溶岩流の流出過程の詳細については,単純に比較はできないことには注意する必要がある.ただし,両噴火の噴出量や噴出率という基礎的な物理量の比較には意味があると考える.
今後の活動について
今後,溶岩は東側と同様に,西側へさらに流動,拡大(埋め立て)していくと考えられる.また,現在の新島の周囲がほとんど溶岩で埋め立てられ,冷却・固化が進んだ場合,マグマは噴火しやすい場所を新たに探し,付近に別の火口を形成する可能性がある.この場合,11月20日頃の様な激しいマグマ水蒸気爆発が再び発生すると考えられる.
今後,溶岩の流出場所・方向,流出量,流出率に着目し,噴火の推移を注意深く観察していく必要がある.
参考資料
- 海上保安庁海洋情報部海域火山データベースhttp://www1.kaiho.mlit.go.jp/GIJUTSUKOKUSAI/kaiikiDB/kaiyo18-2.htm
- 海上保安庁水路部 (1993) 5万分の1沿岸の海の基本図海底地形地質調査報告書「西之島」, p. 47.
- 国土地理院における西之島付近の噴火活動関連情報http://www.gsi.go.jp/gazochosa/gazochosa60010.html
- Maeno, F. and Taniguchi, H. (2006) Silicic lava dome growth in the 1934-1935 Showa Iwo-jima eruption, Kikai caldera, south of Kyushu, Japan. Bulletin of Volcanology, 68, 673-688.
- 小坂丈予 (1991) 日本近海における海底火山の噴火. 東海大学出版会, p. 279.
(火山噴火予知研究センター:前野 深)
観察日時:2013年11月24日午前11:20-12:05
観察者:中田節也
使用機体:セスナ Citation Encore(朝日新聞社機)
概要
新島の大きさは海上保安庁が観測した11月21日午後の様子と大差なく,約200 m x 100 mの北西—南東方向に伸びた楕円形を呈している。新島の高さは西之島の最高点とほぼ同じ20数mと考えられる。島の北東側では海に約50m突き出した溶岩地形が認められる(写真1, 2)。島全体は台形を呈し,その表面はごつごつした大小の火山弾に覆われている。それに対して島の南東側,南西側では,頂部付近から褐色火山灰の岩肌の比較的滑らかな斜面が出現しており,斜面崩壊が起こったものと考えられる(写真2下)。
噴火の様子
島頂部の火口付近
島の中央部からやや南東よりにある頂部の火口では,数秒から数十秒間隔でストロンボリ式噴火を繰り返えしている。噴煙と火山弾は上空300-400m程度まで噴き上がり,水平距離で約500mまでの範囲に着水している(写真3)。頂部火口は10m程度と小さくなっており,噴火の度に赤熱した溶けた溶岩が噴き上がり,その根元は高さ10m程度までの溶岩噴泉状であることから,火口には小さな溶岩湖が形成されていると考えられる。
北東溶岩流
頂部火口の北東斜面中程にも小さな火口が空いており,頂部火口の爆発直後に後者で小爆発が起こり,火山灰が噴き上がることがある。この小さな火口からも赤熱溶岩が顔をのぞかせる。この火口周辺から北東側の海岸線まで,流れた筋が明らかな,より黒色の溶岩流が認められる(写真2下)。この溶岩流は海岸線でやや古い溶岩部にぶつかり,東に向きを変えて海中に没しており,そこからは白煙が勢い良く上昇している。この溶岩流先端部を含めて北東部に突き出した部分は,21日頃から成長した溶岩流部分で,すでに先端の一部が浸食されたものかもしれない。
※報道関係の方へ:朝日新聞社の協力により撮影しています。写真の引用については、朝日新聞社にお問合せください。
(火山噴火予知研究センター:中田節也)
朝日新聞社の取材機(ジェット)に同乗し、西之島2013年活動の観察を行った。この結果、西之島の南東に火砕丘が形成されていることが判った。
観測日時:2013年11月21日9時13分~31分(観察者/金子)
位置: 西之島新島の海岸線より南東に400~500m(山体の中心)(図1)
大きさ: 長径 約300m,短径 約100m (海面レベルを含む)
高さ: 約20~30m
山体の状況: 火砕丘は北西-南東方向に伸長しており,中心より南東側に火口がある(長径約100m) (図2).溶岩流は認められない.
噴火の状況: 1~2分に一回程度の割合で,マグマ水蒸気爆発に伴う噴煙が上がる(図2) .高さは200~300m程度,コックステールジェットを伴う.白色噴煙は最終的には900m程度の高度まで達している.
変色水: 噴火域の西側一帯に拡がっている(図3).新たな噴火点を示す変色域は認められない.
※位置・サイズ等は目測のため正確さに欠ける
※報道関係の方へ:朝日新聞社の協力により撮影しています。写真の引用については、朝日新聞社にお問合せください。
(火山噴火予知研究センター:金子隆之)
Utokyo Research 2017に地震研の研究が掲載されました
東京大学広報戦略部が刊行しているUtokyo Research 2017に、地震研が取り組んでいる海底地震観測について掲載されました。
記事は、2016年3月に、Utokyo ResearchのウェブサイトでFeature Storiesに載ったもので、篠原雅尚教授が取材を受けたものです。
Utokyo Research2016/03/08:震源の近くへ ~海の底で起きる地震を海の底で観測する~

地震という現象を正しく理解するために、震源近くで観測する--。その目的を果たすため、地震研究所は海底で頻発する地震を観測できるシステムを長年開発してきました。このシステムは、2011年の東北地方太平洋沖地震でも活かされましたが、観測の精度が高まるほど、地震のメカニズムはそう単純ではないことも見えてきました。
Utokyo Research 2017:2016年にUtokyo Researchのウェブサイトに掲載された特集記事やウェブサイトに掲載された印象的な画像を通して、2016年に行われた東京大学の研究活動を紹介する、東京大学広報戦略本部が発行している刊行物です。
地震火山史料連携研究機構 発足
地震研究所と史料編纂所が連携する新たな機構:地震火山史料連携研究機構 が、発足しました。
地震・火山に関する理学・工学的な観測・研究を行う地震研究所と、前近代日本史史料の蒐集・研究・編纂を行う史料編纂所が連携し、近代以前に発生した地震・火山に関する史料を収集・分析し、データベースを構築して公開するため、地震火山史料連携研究機構が発足しました。文理融合研究により、史料から新たな理学的価値を引き出し、近代的な計器観測では得られない歴史時代の災害のデータが得られ、その成果は社会的にも重要な地震や火山噴火の長期的予測にも活かされます。両研究所は全国共同利用・共同研究拠点であり、その成果は全国的にも波及することが期待されます。

地震研の研究成果が東大HPに掲載
地震研究所の研究成果が、東京大学ホームページのトップスライドに掲載されました。
3月23日に出版された科学誌”Nature Index 2017 Japan”に、東京大学が世界をリードする最先端研究の紹介記事を掲載。記事内では、本学の卓越した国際的研究を発信する目的で、弊所の田中宏幸教授を中心としたグループによる研究「ミュオグラフィ」が紹介されています。
東京大学ホームページ:http://www.u-tokyo.ac.jp/index_j.html
ミュオグラフィ:MUOGRAPHERS 2016
*Nature Indexは、シュプリンガー・ネイチャー社が発刊している特別企画冊子です。